ボーカル音程モニター(Vocal Pitch Monitor)では、ピッチ推定に自己相関関数を使用しているが、精度を高めるために、FFTの値も使用している。
離散フーリエ変換(FFT)で、スペクトル推定の分解能を高めるために、ゼロパディングという手法が用いられる。
ここでは、ゼロパディングにより、スペクトル推定の精度がどのように変わるかを検証する。
まずは窓長として4096として、435Hzと440Hzの正弦波を含む信号をFFTでスペクトル推定すると以下のようなグラフとなる。
import numpy as np
import matplotlib.pyplot as plt
fs = 44100
size=4096
t = np.arange(0, size) / fs
frq = np.fft.fftfreq(size, 1/fs)
han = np.hanning(size)
for f in [435, 440]:
y = np.sin(2 * np.pi * f * t)
Y = np.fft.fft(y*han)
plt.plot(frq, abs(Y))
plt.axis([400, 500, 0, 2000])
plt.show()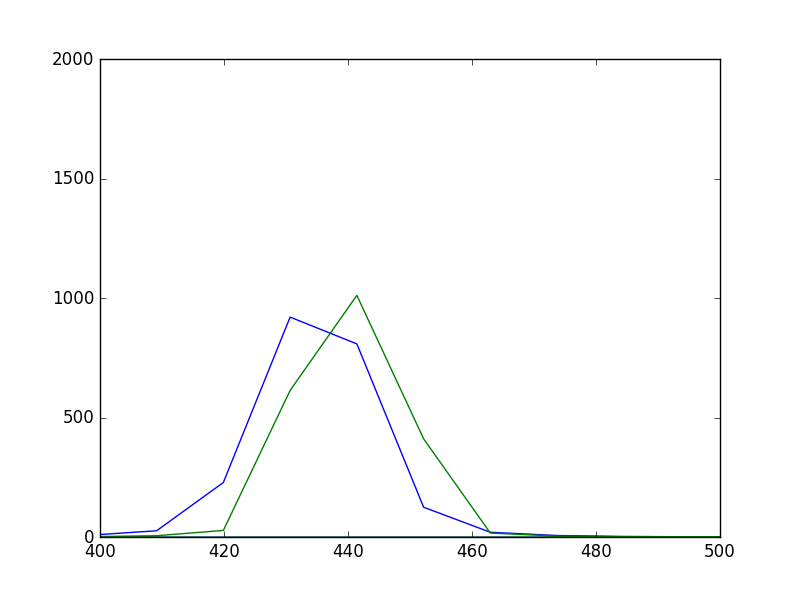
435Hzと440Hzあたりにピークが現れているが、高さが435Hzの方がピークの高さが低くなりサイドローブが大きくなっている。
その理由については以前の日記で記述した。
次に、信号を切り取るフレーム長は4096のままで、窓長を倍の8192にしてゼロパディングを行うと、以下のようなグラフとなる。
size=8192
t = np.arange(0, size) / fs
frq = np.fft.fftfreq(size, 1/fs)
han = np.hanning(size)
for f in [435, 440]:
y = np.sin(2 * np.pi * f * t)
y[size/2:]=0 # ゼロパディング
Y = np.fft.fft(y*han)
plt.plot(frq, abs(Y))
plt.axis([400, 500, 0, 2000])
plt.show()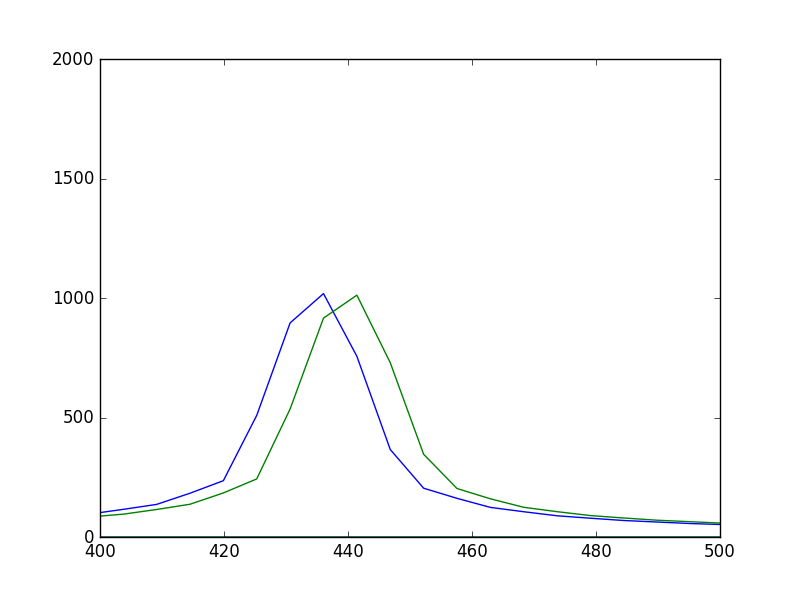
ピークの高さがほぼ同じになっている。
ゼロパディングを行うことでスペクトル推定の精度を高めることができている。
正弦波の信号の周波数を0.1Hz置きに変えて、FFTのピークをプロットすると以下のようなグラフとなる。
size=4096
t = np.arange(0, size) / fs
frq = np.fft.fftfreq(size, 1/fs)
han = np.hanning(size)
fset = np.linspace(400, 500, 1001)
peaks = []
for f in fset:
y = np.sin(2 * np.pi * f * t)
Y = np.fft.fft(y*han)
peak = np.max(abs(Y[:size/2]))
peaks.append(peak)
plt.plot(fset, peaks)
plt.axis([400, 500, 0, 1500])
plt.show()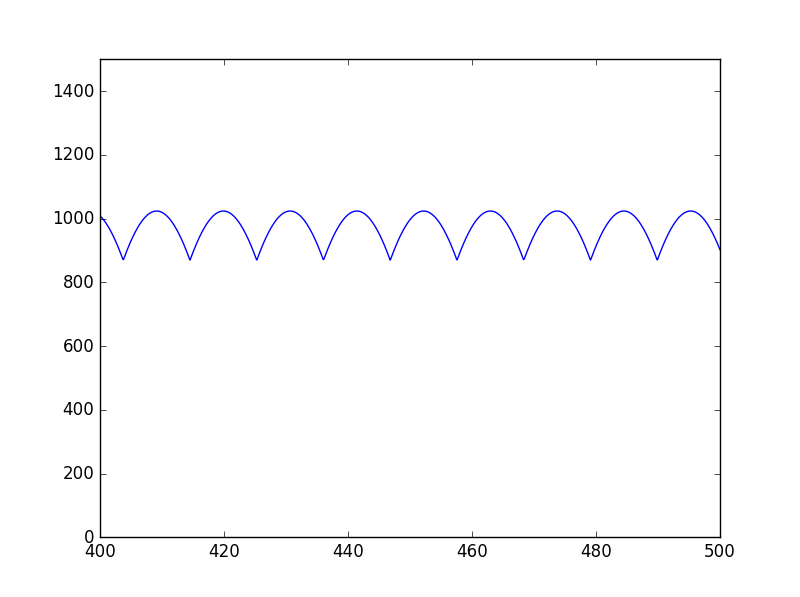
これを、ゼロパディングを行うと以下のようなグラフとなる。
size=8192
t = np.arange(0, size) / fs
frq = np.fft.fftfreq(size, 1/fs)
han = np.hanning(size)
fset = np.linspace(400, 500, 1001)
peaks = []
for f in fset:
y = np.sin(2 * np.pi * f * t)
y[size/2:]=0 # ゼロパディング
Y = np.fft.fft(y*han)
peak = np.max(abs(Y[:size/2]))
peaks.append(peak)
plt.plot(fset, peaks)
plt.axis([400, 500, 0, 1500])
plt.show()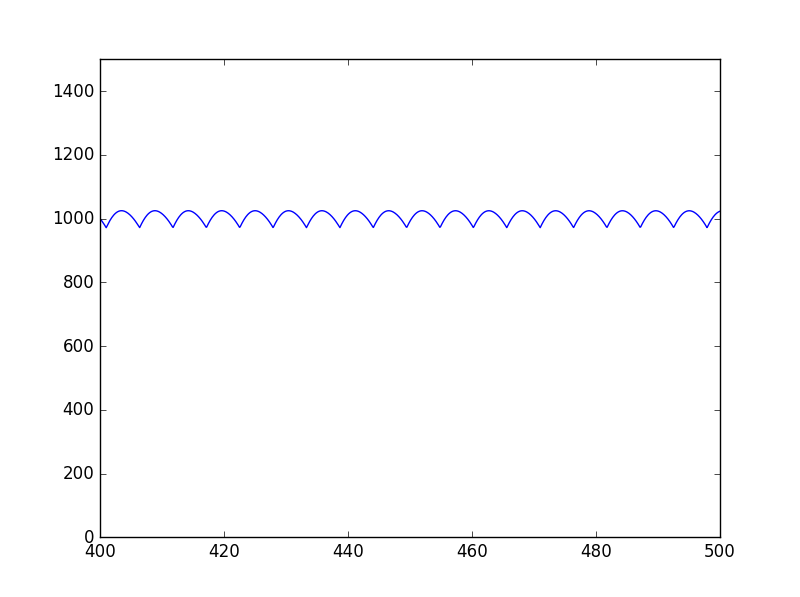
ピークの変動の幅がゼロパディングを行った方が抑えられている。
窓長をさらに倍の16384とすると以下のようなグラフとなる。
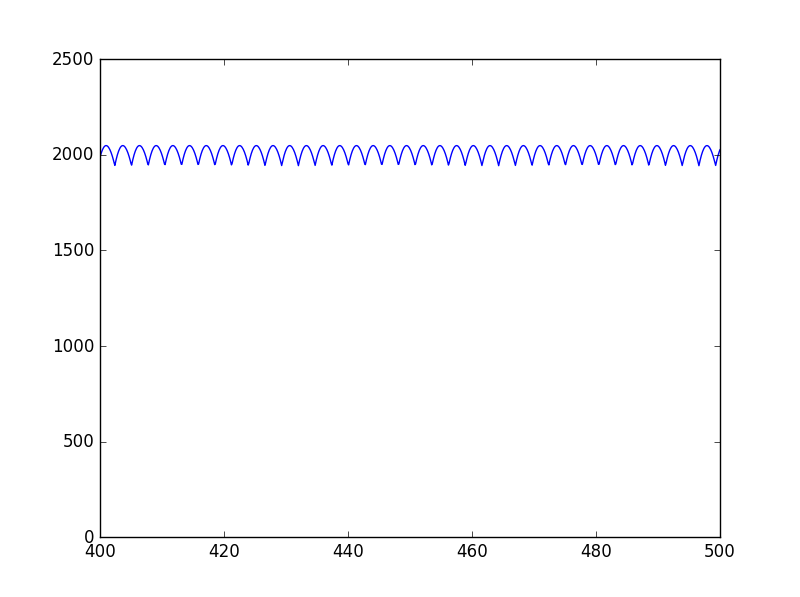
窓長を広げるほど、ピークの変動の幅が抑えられている。
また、ピークの値が大きくなっている。これは、ゼロパティングによりサイドローブが抑えられ、FFTビンがより狭い範囲に集中するためである。
結論
単純に窓長を広げると時間分解能が低くなり、リアルタイムにスペクトル解析するような用途では、周波数分解能とのトレードオフとなるが、ゼロパティングにより時間分解能を変えずに、スペクトル推定の精度を高めることができる。