自己相関関数とピッチ推定の誤差

ボーカル音程モニター(Vocal Pitch Monitor)では、ピッチ推定に自己相関関数を使用している。

自己相関関数を使用するメリットとしては、

ノイズに強い
低周波数での誤差が少ない

という点があげられる。

逆にデメリットとしては、高周波数の誤差が大きくなる。

ここでは、自己相関関数で推定したピッチと真の周波数との誤差について検証を行う。

自己相関関数でピッチを推定する方法は、以前の日記に書いたので、詳細は省略する。

正弦波の周波数を200Hzから400Hzの範囲で0.1Hz間隔で、自己相関関数で推定したピッチをグラフにすると以下のようになる。

import numpy as np
import matplotlib.pyplot as plt
fs = 44100
size = 4096
t = np.arange(0, size) / fs
han = np.hanning(size)

#ピークピッキング
def pick_peak(data):
    peaks_val = []
    peaks_index = []
    for i in range(2, data.size):
        if data[i-1] - data[i-2] >= 0 and data[i] - data[i-1] < 0:
            peaks_val.append(data[i-1])
            peaks_index.append(i-1)
    max_index = peaks_val.index(max(peaks_val))
    return peaks_index[max_index]

peaks = []
fset = np.linspace(200, 400, 2001)
for f in fset:
    y = np.sin(2 * np.pi * f * t)
    Y = np.fft.fft(y*han)
    acf = np.fft.ifft(abs(Y)**2)
    n = pick_peak(np.real(acf[0:size/2]))
    f0 = fs / n
    peaks.append(f0)
plt.plot(fset, peaks)
plt.show()

f:id:TadaoYamaoka:20170107162958p:plain
横軸が真の周波数(Hz)、縦軸が推定したピッチの周波数(Hz)

グラフが階段状になっており、周波数が高いほど、階段の間隔が広くなっていることがわかる。

誤差の値をグラフにすると以下のようになる。

# 誤差(Hz単位)
errors = []
fset = np.linspace(200, 400, 2001)
for f in fset:
    y = np.sin(2 * np.pi * f * t)
    Y = np.fft.fft(y*han)
    acf = np.fft.ifft(abs(Y)**2)
    n = pick_peak(np.real(acf[0:size/2]))
    f0 = fs / n
    errors.append(f0 - f)
plt.plot(fset, errors)
plt.show()

f:id:TadaoYamaoka:20170107163445p:plain

周波数が高いほど、周期的に誤差が大きくなっていることがわかる。

音楽では、ピッチの精度の単位としてcentが使用される。平均律の半音を100centとする単位である。

先ほどの誤差をcent単位とすると以下のようになる。(周波数の範囲を、100Hzから900Hzとした。)

# 誤差(cent単位)
import math
errors = []
fset = np.linspace(100, 900, 8001)
for f in fset:
    y = np.sin(2 * np.pi * f * t)
    Y = np.fft.fft(y*han)
    acf = np.fft.ifft(abs(Y)**2)
    n = pick_peak(np.real(acf[0:size/2]))
    f0 = fs / n
    cent = (math.log(f0, 2) - math.log(f, 2)) * 12 * 100
    errors.append(cent)
plt.plot(fset, errors)
plt.show()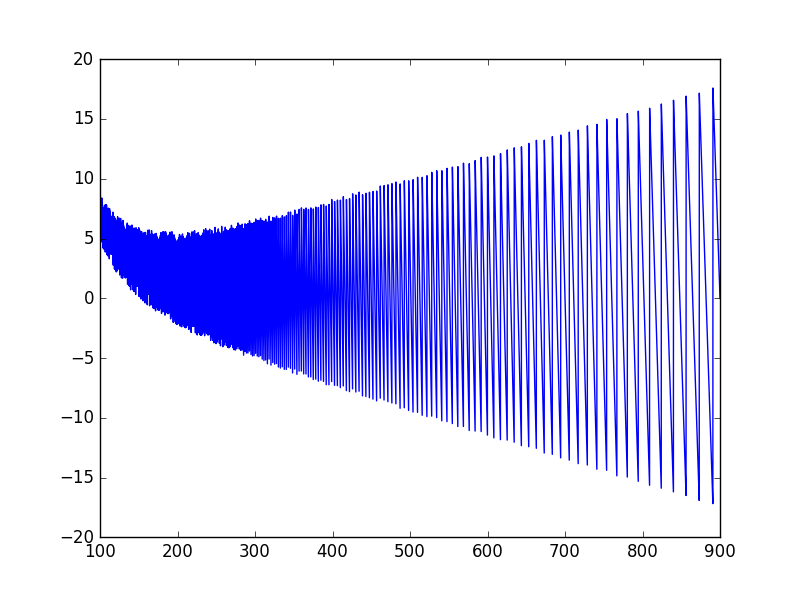

f:id:TadaoYamaoka:20170107165103p:plain

900Hz付近では、誤差が17.5centくらいになっている。
900Hzは、A4=440Hzとした場合の、A5あたりの音階で、女性ボーカルの最高音あたりの音域になる。

音楽の用途としては誤差17.5centは大きい値であり、このままではピッチ推定の精度としては不十分である。

ゼロパディング

前回の日記で、離散フーリエ変換(FFT)でスペクトル推定の精度を高めるために、ゼロパディングという手法が有効であることを説明した。

ここでは、自己相関関数をFFTを使用して計算する際にゼロパディングを行った場合、自己相関関数の誤差がどのように変化するか検証を行う。

窓長を4096の2倍の8192にして、ゼロパディングを行った場合の自己相関関数で推定したピッチをグラフにすると以下のようになる。

# ゼロパディング
size=8192
t = np.arange(0, size) / fs
han = np.hanning(size)

peaks = []
fset = np.linspace(200, 400, 2001)
for f in fset:
    y = np.sin(2 * np.pi * f * t)
    y[size/2:]=0 # ゼロパディング
    Y = np.fft.fft(y*han)
    acf = np.fft.ifft(abs(Y)**2)
    n = pick_peak(np.real(acf[0:size/2]))
    f0 = fs / n
    peaks.append(f0)
plt.plot(fset, peaks)
plt.show()

f:id:TadaoYamaoka:20170108092332p:plain

誤差をHzで示したグラフは以下のようになる。

# 誤差(Hz単位)
errors = []
fset = np.linspace(200, 400, 2001)
for f in fset:
    y = np.sin(2 * np.pi * f * t)
    y[size/4:]=0 # ゼロパディング
    Y = np.fft.fft(y*han)
    acf = np.fft.ifft(abs(Y)**2)
    n = pick_peak(np.real(acf[0:size/2]))
    f0 = fs / n
    errors.append(f0 - f)
plt.plot(fset, errors)
plt.show()

f:id:TadaoYamaoka:20170108092615p:plain