以前の日記で、自己相関関数でのピッチ推定の誤差について検証した。
自己相関関数で求めたピッチは、高周波数で誤差が大きくなることを示した。
ここでは、それを改善する方法について検証する。
自己相関関数のピークの位置をnとすると、周波数fは以下の式で計算できる。
は、サンプリング周波数
自己相関関数は、周期的な関数となるため、ピークの整数倍の位置にもピークが現れる。
つまり、ピークのN倍の位置から周波数を求めて、N倍することでも周波数fを求めることができる。
周波数fは、nの逆数の関数であるため、nが大きいほどピッチの誤差が小さくなる。
N倍の位置のピークを使って周波数fを求める式は以下のようになる。
N倍の位置のピークを使って、ピッチを推定した場合、誤差がどれくらい抑えられるか検証する。
前回の日記で検証した、N倍しないピークを使ったときの誤差と比較するため、周波数の範囲を100Hzから900Hzとして、cent単位で誤差を求める。
import numpy as np
import matplotlib.pyplot as plt
fs = 44100
size = 4096
t = np.arange(0, size) / fs
han = np.hanning(size)
#ピークピッキング
def pick_peak(data):
peaks_val = []
peaks_index = []
for i in range(2, data.size):
if data[i-1] - data[i-2] >= 0 and data[i] - data[i-1] < 0:
peaks_val.append(data[i-1])
peaks_index.append(i-1)
max_index = peaks_val.index(max(peaks_val))
return peaks_index[max_index]
import math
errors = []
fset = np.linspace(100, 900, 8001)
for f in fset:
y = np.sin(2 * np.pi * f * t)
Y = np.fft.fft(y*han)
acf = np.fft.ifft(abs(Y)**2)
n = pick_peak(np.real(acf[0:size/2]))
n1 = n
for N in range(2, int(size / 2 / n1) - 1):
nn = int(n*N)-10 + pick_peak(np.real(acf[int(n*N)-10:int(n*N)+10]))
n = nn / N
f0 = fs / n
cent = (math.log(f0, 2) - math.log(f, 2)) * 12 * 100
errors.append(cent)
plt.plot(fset, errors)
plt.show()
Nは、ピークのnの整数倍とした場合、誤差が大きくピークの位置からずれるため、2倍、3倍と順番にピークの位置を調べてn/Nの値でnを更新している。
Nの上限は、自己相関関数のフレーム長/2を超えない範囲としている。
比較のために、前回の日記で検証した誤差のグラフを示す。
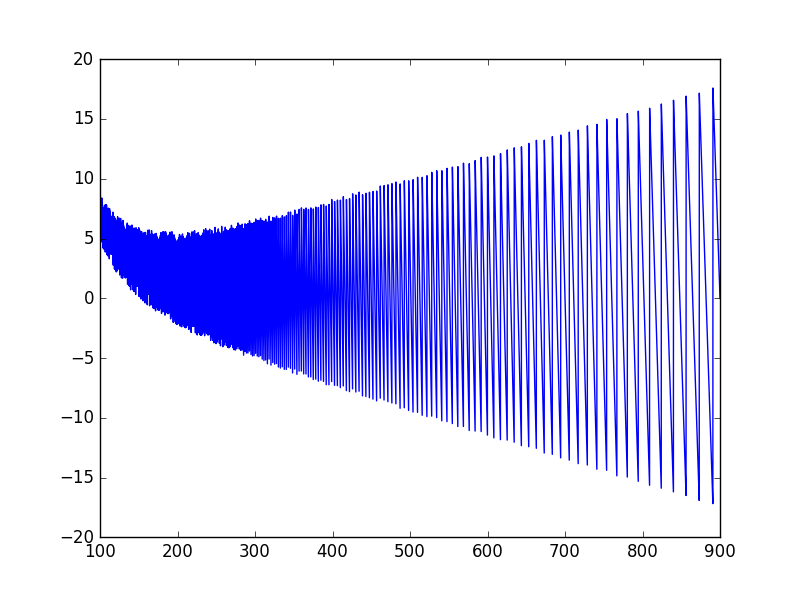
N倍の位置のピークからピッチ推定した場合、周波数が高くなっても誤差が増えていない。一方、N倍しないピークを使ってピッチ推定した場合は、周波数が高くなるほど誤差が増えている。
N倍の位置のピークからピッチ推定した場合の誤差は、-6.9~7.8centの範囲に抑えられている。
音楽のチューニング用途としては1cent程度までの精度が必要である。
それからするとまだ誤差が大きい。
さらに誤差を小さくするには、Nの値をさらに大きい値にするなどの対応が必要となる。
そのためには、フレーム長を大きくするなどの対応が必要となる。