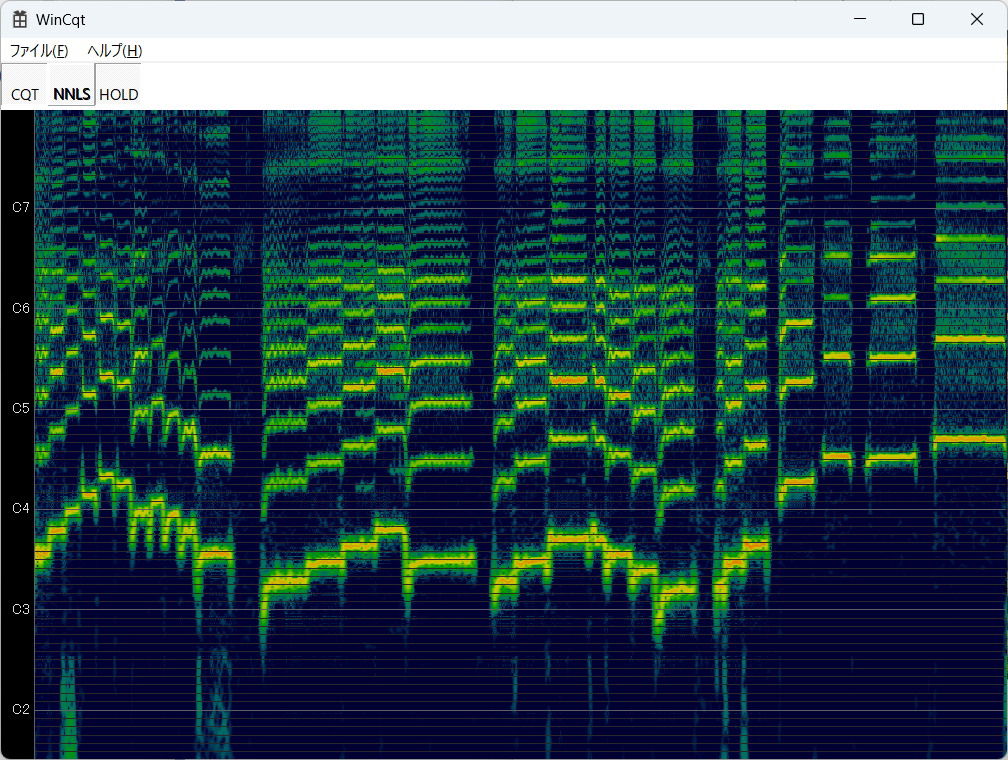
CQTで和音を解析するその２ - TadaoYamaokaの開発日記

前回 Pythonで実装したNNLSをWindowsプログラムに組み込んで、リアルタイムで処理できるか検証する。

NNLSの実装

Pythonでは、scipy.optimize.nnlsを使用したが、C++に組み込むため、Lawson–Hansonのアルゴリズムを独自実装した(GPT-5で実装)。

static void nnls_lawson_hanson_colmajor(
    const double* A, int m, int n,       // A: m×n（列優先）A[j*m + i] = A_ij
    const double* b,                      // b: m
    std::vector<double>& x,               // x: n（出力）
    std::vector<double>& workAx,          // Ax: m
    std::vector<double>& workRes,         // r = b - A x: m
    std::vector<double>& workW,           // w = A^T r: n
    std::vector<int>& passive,            // 1=Passive(P), 0=Active(Z)
    std::vector<int>& active              // 1=Active(Z), 0=Passive(P)
) {
    const int MAX_IT = 3 * n + 5;
    const double TOL = 1e-10;

    x.assign(n, 0.0);
    passive.assign(n, 0);
    active.assign(n, 1);

    // w = A^T b
    workAx.assign(m, 0.0);
    workRes.assign(m, 0.0);
    workW.assign(n, 0.0);
    for (int j = 0; j < n; ++j) {
        double dot = 0.0;
        const double* col = A + j * m;
        for (int i = 0; i < m; ++i) dot += col[i] * b[i];
        workW[j] = dot;
    }

    int it = 0;
    while (it++ < MAX_IT) {
        // Z（active）から最大正の w を持つ列を選択
        double wmax = 0.0; int t = -1;
        for (int j = 0; j < n; ++j) if (active[j] && workW[j] > wmax) { wmax = workW[j]; t = j; }
        if (t < 0 || wmax <= TOL) break; // 収束

        passive[t] = 1; active[t] = 0;

        // 反復内ループ：負成分が出たら P→Z に戻す
        std::vector<int> Pidx; Pidx.reserve(n);
        for (int j = 0; j < n; ++j) if (passive[j]) Pidx.push_back(j);

        // 最小二乗（正規方程式）を P のみで解く
        std::vector<double> G, g;
        auto solve_on_P = [&](std::vector<double>& xP) -> bool {
            const int p = (int)Pidx.size();
            if (p == 0) return false;
            G.assign(p * p, 0.0); g.assign(p, 0.0);
            // G = A_P^T A_P, g = A_P^T b
            for (int a = 0; a < p; ++a) {
                int ja = Pidx[a];
                const double* colA = A + ja * m;
                for (int b2 = a; b2 < p; ++b2) {
                    int jb = Pidx[b2];
                    const double* colB = A + jb * m;
                    double s = 0.0;
                    for (int i = 0; i < m; ++i) s += colA[i] * colB[i];
                    G[a * p + b2] = G[b2 * p + a] = s;
                }
                double sb = 0.0;
                for (int i = 0; i < m; ++i) sb += colA[i] * b[i];
                g[a] = sb;
            }
            // xP ← 解
            xP = g;
            if (!cholesky_solve_spd(G, p, xP)) return false;
            return true;
        };

        // 旧解（P成分）
        std::vector<double> x_old = x;
        for (;;) {
            // 解候補
            std::vector<double> xP;
            if (!solve_on_P(xP)) break;

            // 候補を全成分ベクトルへ詰める
            std::vector<double> xCand(n, 0.0);
            for (int k = 0; k < (int)Pidx.size(); ++k) xCand[Pidx[k]] = xP[k];

            // すべて非負なら採用
            bool allPos = true;
            for (int k = 0; k < (int)Pidx.size(); ++k) if (xCand[Pidx[k]] <= 0.0) { allPos = false; break; }
            if (allPos) { x.swap(xCand); break; }

            // α を求めて0に落ちる変数を Z へ戻す
            double alpha = 1.0;
            for (int k = 0; k < (int)Pidx.size(); ++k) {
                int j = Pidx[k];
                if (xCand[j] <= 0.0) {
                    double denom = xCand[j] - x_old[j];
                    if (denom != 0.0) {
                        double a = x_old[j] / (x_old[j] - xCand[j]);
                        if (a > 0.0 && a < alpha) alpha = a;
                    }
                }
            }
            for (int j = 0; j < n; ++j) x[j] = x_old[j] + alpha * (xCand[j] - x_old[j]);

            // 0 になったものを Z へ
            for (int k = 0; k < (int)Pidx.size(); ++k) {
                int j = Pidx[k];
                if (x[j] <= 1e-16) { x[j] = 0.0; passive[j] = 0; active[j] = 1; }
            }
            // P の再構成
            x_old = x;
            Pidx.clear(); for (int j = 0; j < n; ++j) if (passive[j]) Pidx.push_back(j);
            if (Pidx.empty()) break;
        }

        // w = A^T (b - A x)
        std::fill(workAx.begin(), workAx.end(), 0.0);
        for (int j = 0; j < n; ++j) if (x[j] != 0.0) {
            const double* col = A + j * m;
            double cj = x[j];
            for (int i = 0; i < m; ++i) workAx[i] += col[i] * cj;
        }
        for (int i = 0; i < m; ++i) workRes[i] = b[i] - workAx[i];
        for (int j = 0; j < n; ++j) {
            if (!active[j]) { workW[j] = 0.0; continue; }
            const double* col = A + j * m;
            double dot = 0.0;
            for (int i = 0; i < m; ++i) dot += col[i] * workRes[i];
            workW[j] = dot;
        }
    }
}