以前の日記で、自己相関関数はウィーナー=ヒンチンの定理でFFTを使って高速に計算できることを書いた。
自己相関関数は、同じ波形データ同士をずらしながら掛け合わせた値の合計であることを説明したが、その定義通り計算する場合は窓関数は特に必要ない。
しかし、ウィーナー=ヒンチンの定理でFFTを使って計算する場合は、窓関数の有無によって自己相関関数の減衰の仕方が変わってくるため注意が必要である。
そのことを、具体的な例で示す。
280Hzの正弦波の自己相関をFFTを使って計算すると以下のようになる。
import numpy as np import matplotlib.pyplot as plt fs = 44100 size = 4096 t = np.arange(0, size) / fs f = 280 y = np.sin(2.0 * np.pi * f * t) Y = np.fft.fft(y) acf = np.fft.ifft(abs(Y)**2) plt.plot(acf[0:size/2]) plt.axis([0, size/2, min(acf), max(acf)]) plt.show()
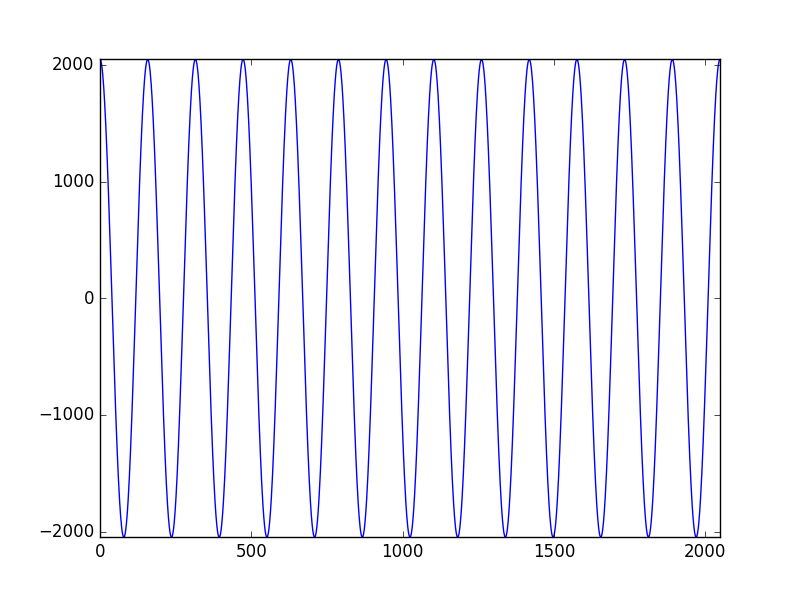
自己相関は、横軸が右に進むほど減衰する関数であるが、減衰していない。
自己相関をscipyの関数で計算すると以下のようになる。
import scipy.signal as sig cor = sig.correlate(y, y, mode="full") plt.plot(cor[cor.size/2:]) plt.axis([0, cor.size/2, min(cor ), max(cor )]) plt.show()

こちらは減衰している。
窓関数を使用すると以下のようになる。
han = np.hanning(size) Y = np.fft.fft(y * han) acf = np.fft.ifft(abs(Y)**2) plt.plot(acf[0:size/2]) plt.axis([0, size/2, min(acf), max(acf)]) plt.show()
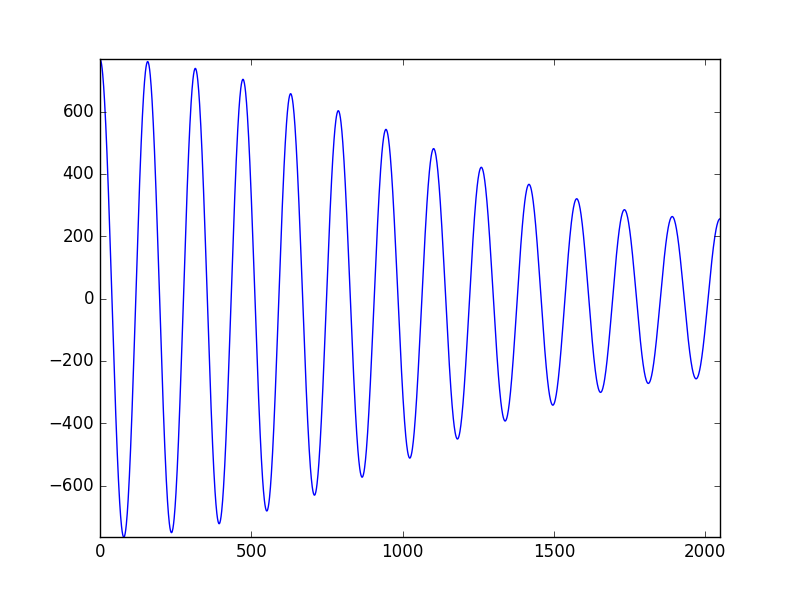
縦軸の値は小さくなってしまうが、減衰する関数となっている。
別の周波数では、このような現象は起きない。
285Hzでは以下のようになる。
f = 285 y = np.sin(2.0 * np.pi * f * t) Y = np.fft.fft(y) acf = np.fft.ifft(abs(Y)**2) plt.plot(acf[0:size/2]) plt.axis([0, size/2, min(acf), max(acf)]) plt.show()

こちらは窓関数を使用しなくても減衰する関数となっている。
波形データの周波数によって、減衰する場合としない場合で規則性があるか調べてみた。
200Hzから400Hzの間で、0.1Hz置きに自己相関の10番目のピークの値をグラフにすると以下のようになる。
peaks = [] fset = np.linspace(200, 400, 2001) for f in fset: y = np.sin(2 * np.pi * f * t) Y = np.fft.fft(y*han) acf = np.fft.ifft(abs(Y)**2) n = int(fs / f * 10) peaks.append(acf[n]) plt.plot(fset, peaks) plt.show()
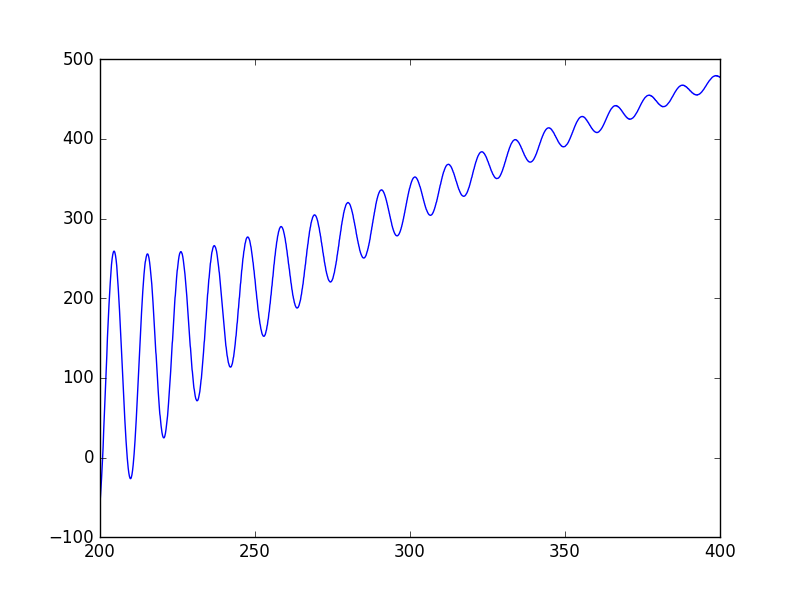
約10.8Hz間隔でピークが現れている。
10.8Hzは周波数分解能(fs/size)とほぼ一致おり、ちょうど周波数分解能の整数倍の位置でピークになっている。
周波数分解能の整数倍の場合、FFTの値がきれいな一本のスペクトルの形になるので、そのパワースペクトルの逆フーリエ変換は、減衰しないきれいな正弦波となる。
元々、ウィーナー=ヒンチンの定理で計算する自己相関は、無限に続く周期関数において成り立つ式であり、減衰しない関数となるのが正しい。
FFTを用いて計算した場合、減衰しない方が正しいのであり、減衰する方が離散化の影響を受けた結果となる。
周波数が整数倍の場合に窓関数を使用した場合に、減衰する関数となるのは、窓関数自体の減衰する特性の影響が現れためである。
逆に、周波数が周波数分解能の整数倍からはずれた場合は、窓関数を使用すると、使用しない場合より減衰しない関数となる。
上記の285Hzの場合に窓関数を使用すると以下のようになる。
f = 285 y = np.sin(2.0 * np.pi * f * t) Y = np.fft.fft(y*han) acf = np.fft.ifft(abs(Y)**2) plt.plot(acf[0:size/2]) plt.axis([0, size/2, min(acf), max(acf)]) plt.show()

窓関数を使用しない場合に比べて、減衰が緩やかになっている。
ウィーナー=ヒンチンの定理で自己相関関数を計算する場合は、このような現象が現れることに注意が必要である。