大規模言語モデルで将棋AIを作る その５（Transformerのスクラッチ実装）

前回までは、TransformerをPyTorch標準のnn.TransformerEncoderを使用して実装していた。
位置エンコーダに「Relative Position Representations」などを使用しようとした場合、Muliti head self-attentionの計算を変更する必要がある。
そのため、Muliti head self-attentionをnn.TransformerEncoderを使用せず、実装する必要がある。

PyTorch標準の実装

nn.TransformerEncoderをONNXにして、Netronで表示すると以下のようになっていた。

トークン長が可変のため複雑で、あまり実装の参考にできない。
Transformerの論文を参考に定義通り実装することにする。

独自実装

Q、K、Vの計算

ResNetの特徴マップとテンソルの次元が(batch_size, channels, hight, width)になるため、Q、K、Vのテンソルの計算は、カーネルサイズ1x1のConv2dを使うと効率化できる。
また、マルチヘッドは、groupsを使うことで実装できる。
Q、K、Vを1つのConv2Dで計算して、出力をchunkで分割する。

class TransformerEncoderLayer(nn.Module):
    def __init__(self, channels, d_model, nhead, dim_feedforward=256, dropout=0.1, activation=nn.GELU()):
        ...
        self.qkv_linear = nn.Conv2d(channels, 3 * d_model, kernel_size=1, groups=nhead, bias=False)
        self.o_linear = nn.Conv2d(d_model, d_model, kernel_size=1, bias=False)
        ...

    def forward(self, x):
        qkv = self.qkv_linear(x).squeeze(-1)
        q, k, v = qkv.chunk(3, dim=1)
        ...

Scaled dot product attentionの計算

Scaled dot product attentionの計算は、定義の通り計算する。
Conv2dで計算したq, k, vは、次元が(batch_size, d_model, seq_len)になっているので、ヘッドを分割して、matmulの計算用に次元を入れ替える。
Scaled dot product attentionの計算後、次元を元に戻す。

    def forward(self, x):
        ...
        q = q.view(batch_size, self.nhead, self.depth, 81).transpose(2, 3)
        k = k.view(batch_size, self.nhead, self.depth, 81)
        v = v.view(batch_size, self.nhead, self.depth, 81).transpose(2, 3)

        scores = torch.matmul(q, k) / math.sqrt(self.depth)
        attention_weights = F.softmax(scores, dim=-1)
        attention_weights = self.attention_dropout(attention_weights)

        attended = torch.matmul(attention_weights, v)
        attended = attended.transpose(2, 3).contiguous().view(batch_size, self.d_model, 9, 9)
        attended = self.o_linear(attended)
        ...

FFNの計算

FFNは通常、2層のLinearで実装するが、カーネルサイズ1x1のConv2dで実装することにする。
Normalizationは、通常Layer normを使用するが、シーケンス長が固定のため、Batch Normalizationで実装する。
Normalizationの位置は、Post-normとする。

class TransformerEncoderLayer(nn.Module):
    def __init__(self, channels, d_model, nhead, dim_feedforward=256, dropout=0.1, activation=nn.GELU()):
        ...
        self.linear1 = nn.Conv2d(d_model, dim_feedforward, kernel_size=1, bias=False)
        self.linear2 = nn.Conv2d(dim_feedforward, channels, kernel_size=1, bias=False)
        self.final_dropout = nn.Dropout(dropout)
        self.norm1 = nn.BatchNorm2d(d_model)
        self.norm2 = nn.BatchNorm2d(channels)

    def forward(self, x):
        ...
        x = self.norm1(attended + x)
        feedforward = self.activation(self.linear1(x))
        feedforward = self.linear2(feedforward)
        feedforward = self.final_dropout(feedforward)
        x = self.norm2(feedforward + x)

        return x

学習結果

独自実装したTransformerEncoderLayerで学習できるか確認した。
ネットワーク構成は、前回と同じResNet12ブロック256フィルタの後に、Transformer8層とする。

データは前回と同じで、4エポック学習した。

精度

	nhead	feed forward	活性化関数	val loss	policy acc.	value acc.
ResNet				2.5547	0.4136	0.6714
PyTorch標準	8	256	gelu	2.5627	0.4124	0.6769
独自実装	8	256	gelu	2.5501	0.4145	0.6753

PyTorch標準と同等の精度になった。
若干精度が良くなっているが、シードを固定していないためランダムの影響と考える。
FFNをBatchNormalizationにしてPost-normにしたことも影響しているかもしれない。

学習時間

	nhead	feed forward	活性化関数	学習時間
ResNet				1:37
PyTorch標準	8	256	gelu	1:58
独自実装	8	256	gelu	2:14

学習時間は標準実装に比べて遅くなった。
PyTorch標準のnn.TransformerEncoderは、内部はC++言語で効率的に実装されているため、Pythonで個々の演算を実装すると遅くなるのはある程度仕方がないが、まだ最適化の余地はあるかもしれない。

モデル改良

ONNX

モデルをONNXにして、Multi head attentionの構造を確認すると以下のようになっていた。

想定よりも複雑になっていた。
以下の部分で、余計な演算が発生している。

        qkv = self.qkv_linear(x).squeeze(-1)
        q, k, v = qkv.chunk(3, dim=1)

また、バッチサイズを、batch_size = x.size(0)で取得している部分でも演算が発生している。

        batch_size = x.size(0)
        ...
        q = q.view(batch_size, self.nhead, self.depth, 81).transpose(2, 3)
        k = k.view(batch_size, self.nhead, self.depth, 81)
        v = v.view(batch_size, self.nhead, self.depth, 81).transpose(2, 3)

改良

固定値で演算が不要な部分は、演算が発生しないように修正した。

        qkv = self.qkv_linear(x)
        q, k, v = qkv.split((self.d_model, self.d_model, self.d_model), dim=1)

        q = q.view(-1, self.nhead, self.depth, 81).transpose(2, 3)
        k = k.view(-1, self.nhead, self.depth, 81)
        v = v.view(-1, self.nhead, self.depth, 81).transpose(2, 3)

ONNXは、以下のように余計な演算がなくなりシンプルな構成になった。

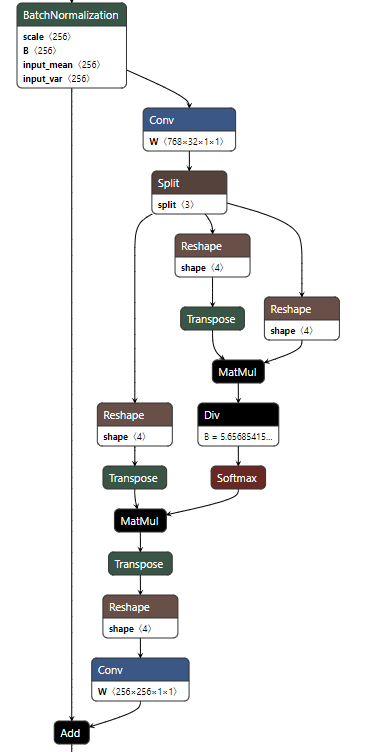
精度

精度が変わっていないか確認した。

	nhead	feed forward	活性化関数	val loss	policy acc.	value acc.
ResNet				2.5547	0.4136	0.6714
PyTorch標準	8	256	gelu	2.5627	0.4124	0.6769
独自実装	8	256	gelu	2.5501	0.4145	0.6753
改良版	8	256	gelu	2.5473	0.4132	0.6763

若干精度が良くなっているが、シードを固定していないためランダムの影響と考える。

学習時間

	nhead	feed forward	活性化関数	学習時間
ResNet				1:37
PyTorch標準	8	256	gelu	1:58
独自実装	8	256	gelu	2:14
改良版	8	256	gelu	2:11

学習時間はほぼ同じである。

まとめ

TransformerをPyTorch標準のnn.TransformerEncoderを使わずに実装した。
PyTorch標準と比べて同等の精度となり、想定通り実装できていることが確認できた。

次は、相対位置エンコーダを実装したい。