将棋AI実験ノート：自己対局時のノードの再利用

以前に、dlshogiの自己対局でノードの再利用を行うと、テスト損失が上昇する（過学習する）という問題が起きたことを書いた。

方策の分布を学習するようにしたため、問題も起きにくくなっている可能性があるので、ノードの再利用（ルートノードはクリア）を行うオプションを追加した（--reuseオプション）。

比較

再利用ありとなしで1.5億局面生成して、精度を比較してみた。
学習済みモデルに対して、方策の分布を学習するようにして追加学習を行った。
8回測定を行い平均をとった。
テストデータに、floodgateのレート3500以上の対局の棋譜からサンプリングした856,923局面を使用した。

再利用	テスト方策損失	テスト価値損失	テスト方策エントロピー
なし	1.61784394	0.466380099	1.305249458
あり	1.60676804	0.463773155	1.315900149

考察

再利用ありの方が、方策、価値ともにテスト損失が下がっており、精度が上がっている。
以前に起きたようなテスト方策エントロピーの低下も起きていない。

強さの比較

持ち時間1分1秒加算、2GPUで対局して強さを比較した結果は、以下の通り。

   # PLAYER           :  RATING  ERROR  POINTS  PLAYED   (%)  CFS(%)    W    D    L  D(%)
   1 reuse            :    13.9   10.5   913.0    1725    53      61  821  184  720    11
   2 noreuse          :    11.3   10.4   903.5    1725    52     100  814  179  732    10
   3 susho3kai18th    :   -25.1   10.3   770.5    1724    45     ---  693  155  876     9

有意差はなかった。

生成速度

GPUあたり4スレッド、8GPU

再利用	nodes/sec
なし	276.1
あり	153.9

GPUあたりのスレッド数が同一だと、生成速度は55.7%になった。
ゲーム木が深くなるため、ノード選択の回数が増えるためと考えられる。
再利用する場合は、GPUあたりのスレッド数を増やす必要がある（その分ハードの制約が厳しくなる）。

まとめ

自己対局時にノードを再利用することで、テスト局面に対する精度が上がることが確かめられた。
ただし、精度の向上が強さには反映されることは測定できていない（持ち時間をかえる、強化学習を世代を増やすなど条件を変えてみる必要がある）。

ノードを再利用する局面の生成速度が落ちるため、質をとるか量をとるかのトレードオフになる（どっちが良いかは確認できていない）。

将棋AI実験ノート：方策の学習に温度パラメータを導入

以前にdlshogiで方策の分布を学習できるようにしたが、方策の分布を学習したモデルで対局すると、指し手のみを学習したモデルよりも弱くなるという問題が起きている。
温度パラメータの調整である程度強くできたが、指し手のみを学習したモデルには及んでいない。
分布を学習することで、探索する手が広がるため、探索の深さが浅くなることが原因と考えている。

この特性は、強化学習を行う際には、新しい手を探索しやすくなるため有効に働く。
モデルの方策と価値のfloodgateの棋譜に対する精度も高くなることが分かっている。
世界コンピュータ選手権向けのモデルでは、方策の分布を学習して強化学習したモデルで生成した指し手を、別のモデルで学習するという手法をとった。

温度パラメータで調整

指し手のみを学習する際、方策を記録したhcpe3フォーマットから、指し手のみを記録したhcpeフォーマットに変換を行っていたが、これを温度パラメータで調整できるようにした。
学習する方策を、ルートの子ノードaの訪問回数をN(a)、温度として、

として、学習する。

温度が0の場合は、指し手のみを学習する、温度が1の場合は、方策の分布を学習する。
温度が1より低い場合は、より訪問回数が多い手の確率が高くなり、温度が1より大きい場合はより確率が均一になる。

温度パラメータを変えて学習

温度パラメータを変えて学習した際の、テスト損失、テストエントロピーを比較した。
学習データにはdlshogiの強化学習で生成した4千万局面を使用し、既存モデルに追加学習した。
8回測定を行い平均をとった。
テストデータに、floodgateのレート3500以上の対局の棋譜からサンプリングした856,923局面を使用した。

温度	テスト方策損失	テスト価値損失	テストエントロピー
0	1.817141809	0.52847061	1.350876433
0.3	1.770466749	0.527390403	1.354992663
0.5	1.739721565	0.52895042	1.393257098
0.8	1.704725165	0.523376935	1.489995551
0.9	1.690805215	0.523304745	1.555975463
1	1.681393201	0.522688101	1.592738526
1.1	1.680972238	0.523270845	1.639763045

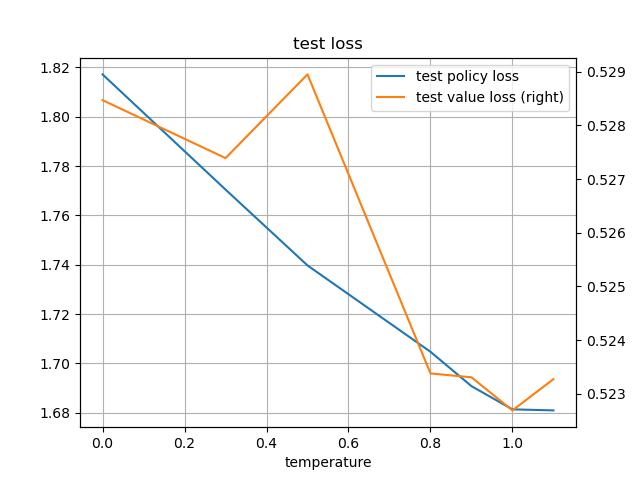
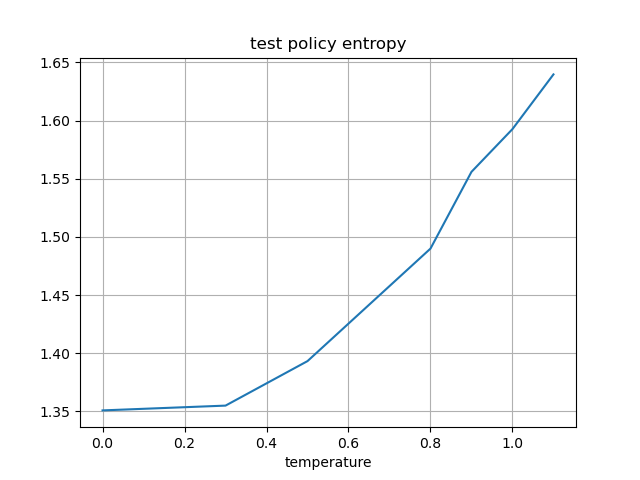
考察

温度が1の場合に価値の損失が一番低くなる。
また、温度が上がるほどエントロピーが上昇する（確率が均一に近づく）。
上で述べた性質が実験からも確認できた。

強さの比較

温度1と温度0.9で学習したモデルを使用して強さを比較した。
探索パラメータは、温度1で学習したモデル用に調整している。

持ち時間1分、1秒加算

   # PLAYER                 :  RATING  ERROR  POINTS  PLAYED   (%)  CFS(%)    W    D    L  D(%)
   1 gct_075_opt20_tmp09    :     6.6   13.0   592.0    1152    51      65  527  130  495    11
   2 gct_075_opt20_tmp1     :     2.0   12.9   582.5    1155    50      83  519  127  509    11
   3 susho3kai18th          :    -8.6   12.7   554.5    1151    48     ---  501  107  543     9

※gct_075_opt20_tmp09：温度0.9で学習したモデル、gct_075_opt20_tmp1：温度1で学習したモデル

有意差なしという結果になった。
ただし、モデルに合わせて探索パラメータも調整が必要になるので、差が出なかった可能性がある。

まとめ

方策を学習するか、指し手のみを学習するかを温度パラメータで調整できるようにした。
これによって、hcpe3フォーマットからhcpeへの変換が不要になる。
train_hcpe3で、指し手のみの学習もできるようになった。

温度パラメータによって、精度、エントロピーに違いがでることが確認できた。
温度が1の場合は精度が高く、エントロピーが高くなる。温度が0に近づくにつれ精度とエントロピーが下がる。
エントロピーが下がると、探索の幅より深さを優先することになるので、対局では有利に働く場合がある（持ち時間にも依存すると思われる）。

dlshogiの学習部のリファクタリングと各手法の精度比較

世界コンピュータ選手権も終わったので、feature/hcpe3やfeature/hcpe3_averageに分かれていたブランチをmasterに統合して整理した。

リファクタリング

重複局面の平均化や、評価値の補正をオプション(それぞれ--use_averate、--use_evalfix)で有効/無効化できるようにした。

また、hcpeとhcpe3の2つのフォーマットで学習スクリプトを分けていたが、train_hcpe3でどちらも読み込めるようにした。
重複局面の平均化などは、train_hcpe3のみに実装している。

また、train_hcpeのみにあったアクタークリティックとエントロピー正則化を、train_hcpe3でも使用できるようにした（--use_criticと--beta）。

各手法の精度比較

オプションで有効無効を切り替えられやすくなったので、今までちゃんと比較していなかったので、各手法の精度を比較した。

比較対象

条件	説明
hcpe	これまでのtrain_hcpeのデフォルト
hcpe3	train_hcpe3のオプションなし
hcpe3_critic	train_hcpe3の--use_critic --beta 0.001※hcpeと等価
hcpe3_evalfix	train_hcpe3の--use_evalfix
hcpe3_average	train_hcpe3の--use_average
hcpe3_average_evalfix	train_hcpe3の--use_average --use_evalfix
hcpe3_average_evalfix_critic	train_hcpe3の--use_average --use_evalfix --use_critic --beta 0.001

テストデータ

テストデータには、2017年～2018年6月のfloodgateのR3500以上の棋譜からサンプリングした856,923局面(重複なし)を使用した。
シャッフルにより結果が変わるため8回測定して平均を求めている。

精度は、方策、価値(勝率)のテスト損失で比較する。

学習データ

dlshogiの自己対局で生成した4千万局面(重複局面は0.14%)を、既存モデルに追加学習を行った結果を比較する。

比較結果

条件	policy	value
hcpe	1.835472639	0.529408829
hcpe3	1.81209377	0.534351326
hcpe3_critic	1.833132198	0.53397902
hcpe3_evalfix	1.812563669	0.525772249
hcpe3_average	1.816512931	0.534330776
hcpe3_average_evalfix	1.807865608	0.529676239
hcpe3_average_evalfix_critic	1.83458015	0.536404066

考察

hcpeとhcpe3_criticは等価だが、8回測定の平均でも結果には誤差が出ている。
policyとvalueがトレードオフの関係にあり、片方の損失が低くなった場合はもう片方が高く学習される場合がある。

critcの有り無しでは、有りの方がpolicy、valueともに損失が高くなる傾向がある。
アクタークリティックは、方策勾配法で用いられる手法であるため、MCTSの自己対局で生成した教師をオフポリシーで学習する場合には効果がないことが分かった。

averageの有り無しでは、policy、valueともに傾向が見えない。
使用した教師データには、重複がほとんどないデータを用いたためと考えられる。
重複の多い教師データを使用すると、averageなしではpolicyの損失がnanになり学習できない問題があるため、averageは有効にしておいて良いだろう。

evalfixの有り無しでは、valueの損失が小さくなる傾向がある。
前回実験した結果と同様の傾向である。

まとめ

今までブランチで学習手法を分けていたが、masterに統合しオプションで切り替えられようにした。
オプションでオンオフできるようになったので、あらためて各手法の比較を行った結果、MCTSの自己対局ではアクタークリティックは逆効果であることがわかった。
また、重複局面の平均化は重複局面が少ない場合はどちらでもよく、評価値の補正はvalueの損失を下げる効果があることがわかった。
重複が多い場合は、重複局面の平均化がないと学習できないため、常にオンにしておいてよい。
よって、おすすめ設定は、「--use_average --use_evalfix」となる。

あと、今回の結果を受けて、policyのテスト損失にクリティックを使用していたが削除した。
これまでよりも数値が高くでるようになっているので注意（上記の実験結果にも適用されている）。

GCTの学習に使用したデータセットを公開

dlshogi with GCTのWCSC31バージョンのモデルの学習に使用したデータセットを公開します。

https://drive.google.com/drive/u/3/folders/1Lkh4HL0tMx9p3NNbHue9lvh_HOSBGxhv

加納さんのご厚意により、Googleドライブの無料枠を大幅に上回る容量を提供してもらいました。
（いつまで提供できるかは保証できなため、データ取得はお早めに）

ファイルの説明

hcpe3/selfplay_gct-???.hcpe3.xz

• 中盤メインの5億の初期局面集で強化学習したデータ
• 040までは1600playout
• 041～055は1800playout
• 056～070は2000playout
• 071～は2400playout
• hcpe3フォーマット
• 方策の分布を学習したモデルで生成。GCTのモデルはこのデータの一部をhcpeに変換して学習。
• xzで圧縮しているため解凍が必要

hcpe3/selfplay_gct???_floodgate26*.hcpe3.xz

• floodgateの26手目までから作成した初期局面集で強化学習したデータ
• gct???の部分は、selfplay_gct-???のどこまでを学習したモデルで生成したかを表す
• GCTモデルの学習ではほとんど使用していなかった

hcpe3/selfplay_gct???_taya36.hcpe3.xz

• たややん互換局面を初期局面集として強化学習したデータ
• gct???の部分は、selfplay_gct-???のどこまでを学習したモデルで生成したかを表す
• hcpeに変換してGCTモデルの学習に使用した

hcpe3/selfplay_model-0000???_taya36.hcpe3.xz

• たややん互換局面を初期局面集として、GCTのモデルを使用して強化学習したデータ
• model-0000???の部分は、GCTのモデルのバージョン番号を表す
• hcpeに変換してGCTモデルの学習に使用した

aobazero/hcpe

• AobaZeroの棋譜をhcpeに変換したもの
• 電竜戦バージョンのGCTの学習以降もしばらく使用していたが、学習の後半では使用していない
• 序盤の学習に効果があるが、中終盤の質が今一つ

gct/hcpe/play-001

• floodgate/電竜戦/ローカル対局/ローカル対局（棋力計測）から生成したデータ
• _nomateが付くファイルは詰みの局面を除いたもの（除いた方が精度が上がる）

gct/hcpe/selfplay-unique-900xx/selfplay-unique-902xx

• たややん互角局面集での強化学習データ
• GCTの強化学習で生成したデータ
• 学習を安定させるために過去に生成したデータも常に学習に加えていた（効果は未検証）

gct/hcpe/selfplay-unique-901xx/selfplay-unique-903xx

• やねうら互角局面集での強化学習データ
• GCTの強化学習で生成したデータ
• 学習を安定させるために過去に生成したデータも常に学習に加えていた（効果は未検証）

suisho/hcpe

• 水匠の相入玉局面教師（たややんさんには、discord で公開の許可をもらっています。）

大会で使用したモデルについて

hcpe3の方は山岡が作成して、hcpeの方は加納さんの方で生成して、GCTのモデルは加納さんが主に学習を進めて、最後に山岡が生成したファイルも混ぜてお互いで学習して強くなったモデルを採用しています。

公開の目的とか

このデータを生成するために、マシンパワーと労力を費やしています。
ディープラーニングを使ったコンピュータ将棋を始めてみたくても、同じだけのデータを用意するのはかなりハードルが高いと思います。
学習やモデルアーキテクチャにまだまだ工夫の余地があるため、そちらで競い合ってフィードバックしあえる環境を作りたいという思いでデータを公開します。

データ生成にはマシンパワーが必要ですが、学習環境には、TensorCoreのあるGPU1枚か、Google Colab（できればColab Pro）があれば十分です。

新たな人がコンピュータ将棋の開発に参加して、いっしょに盛り上げていってくれることを期待します。

将棋AI実験ノート：自己対局の評価値の補正

Discordで、評価値と勝率を変換する際の以下のシグモイド関数の係数aは、dlshogiはelmo_for_learnの自己対局から求めた756.0864962951762という値を使用しているが、floodgateの棋譜などを学習する場合はもっと低い値になるので補正すべきというやり取りがあった。

floodgateの棋譜から調査

R3800以上の棋譜

実際にどれくらいの値なのか2019年～2020年のR3800以上のfloodgateの棋譜から調べてみたところ、
a = 236.94908509
という結果であった。

R2000以上の棋譜

R2000以上とすると、
a = 398.66185164
という結果であった。

調査に使用したスクリプト：csa_score_value_fit.py · GitHub

Discordでのやり取りの通り、係数aは小さい値になった。
また、レーティングが高いほど、係数aが小さくなる傾向がありそうである。

自己対局の評価値と勝率の関係

dlshogiの自己対局で生成した教師データに対しても、評価値と勝率の係数を調べてみた。
自己対局では評価値はルートノードの訪問回数が最も多い子ノードの平均価値(勝率)を、評価値に変換して記録している。
その際の係数には、a=756.0864962951762を使用しているため、その値に近い値になると考えていた。

しかし、実際に調べてみると、
a = 488.09106542
という結果であった。

調査に使用したスクリプト：hcpe_score_value_fit.py · GitHub

これは、自己対局時の探索で求めた勝率と、実際の対局結果を統計処理した勝率にずれがあることを示している。
係数が小さい方にずれているということは、実際の勝率が探索で求めた勝率よりも高いことを示している。
なぜ係数が小さい方にずれるのかは分からないが、探索で求めた評価値をそのまま学習に使うよりも、実際の勝敗から求めた係数で補正した方がよい可能性がある。

評価値を補正して学習

評価値を勝敗から求めた係数で補正したデータを使用し、dlshogiのモデルを学習して、補正なしの場合とありの場合で、精度を比較した。
テストデータには、2017年～2018年6月のfloodgateのR3500以上の棋譜からサンプリングした856,923局面(重複なし)を使用した。
初期値とデータのシャッフルにより結果が変わるため4回測定して平均を求めている。

精度は、方策、価値(勝率)、Q値(評価値)のテスト損失で比較する。
（正解率は、テストデータのクラスの分布が不均衡だと比較しにくいため、精度の比較には損失の方がよい）

変換に使用したスクリプト：fix_hcpe_eval.py · GitHub

floodgateの棋譜

2019年～2020年のR3800以上のfloodgateの棋譜(6235207局面)の評価値を補正して、初期値から学習した結果は以下の通り。

	方策	価値(勝率)	Q値(評価値)
補正なし	1.70100901	0.656220725	0.688526105
補正あり	1.713669813	0.65317638	0.691249333

補正ありの場合が、価値の損失が小さくなっている。
（その変わり、方策の損失が大きくなっているが、これは、初期値から学習した段階では、方策と価値がトレードオフの関係で学習されるためと考えられる。）

補正を行うことで、価値の精度が上がることを示している。

Q値(評価値)が、補正を行った方が高くなっているのは、テストデータの評価値は補正を行っていないためと考えられる。
テストデータに評価値を補正したデータを使用すると、

	方策	価値(勝率)	Q値(評価値)
補正なし	1.648518813	0.65597565	0.659327383
補正あり	1.659034425	0.65457407	0.65837852

補正ありの方が、Q値(評価値)の損失も小さくなった。

自己対局の棋譜

自己対局で生成した教師データ(4千万局面)の評価値を補正して、学習済みモデルに追加学習を行った結果は以下の通り。

	方策	価値(勝率)	Q値(評価値)
補正なし	0.816202783	0.49896154	0.644653933
補正あり	0.812867498	0.493460893	0.658458863

補正ありの場合が、価値の損失が小さくなっている。
また、方策の損失も小さくなっている。
Q値(評価値)の損失は大きくなっているが、テストデータの評価値の補正を行っていないためである。

テストデータに評価値を補正したデータを使用すると以下の通りになった。

	方策	価値(勝率)	Q値(評価値)
補正なし	0.80054098	0.498679225	0.512195093
補正あり	0.79759852	0.493009955	0.508437538

Q値(評価値)の損失についても小さくなっている。

まとめ

floodgateの評価値と勝率の変換に使用するシグモイド関数の係数は、コンピュータ将棋界隈で知られている600よりも小さい値であることがわかった。
また、自己対局時の探索で求めたPVの平均価値(勝率)と、実際の対局結果の統計から求めた勝率にはずれがあることが確認できた。

どちらのデータも学習に使用する場合、評価値を実際の対局結果から求めた係数で補正することで、価値の精度が向上することが確かめられた。

dlshogiの学習スクリプトにも評価値を自動で補正するオプションを処理を追加する予定である。

dlshogi with GCT（WCSC31バージョン）のWindows版ビルド済みファイル公開

dlshogi with GCT（WCSC31バージョン）のWindows版ビルド済みファイルを公開します。

ダウンロード

Release 第31回世界コンピュータ将棋選手権バージョン · TadaoYamaoka/DeepLearningShogi · GitHub

NVIDIA GPUに対応したTensorRT版と、NVIDIA GPU非搭載のWindows PCでも動作するOnnxRuntime版を含みます。

OnnxRuntime版について

Windows 10 version 1903以降のPCであれば実行可能です。
ただし、探索速度は、TensorRT版にくらべて落ちます。
最高のパフォーマンスを出すには、TensorRT版をTensorCore搭載のNVIDIAのGPU(NVIDIA GeForce 2080Tiなど)で動かすことを推奨します。

同梱しているモデルファイル

model-0000225kai.onnx	比較的オールラウンダー（デフォルト）
model-0000226kai.onnx	たややん互換局面特化

※大会では予行2日目最終戦以外は、model-0000226kai.onnxを使用

検討での使用

ShogiGUIの検討機能で使うには、一部対応できていない機能があります。
「深さ」の指定はできません。
時間無制限でも、UCT_NodeLimitで設定したノード数に達すると探索を終了します。

検討では、設定でDNN_Batch_Sizeを256など大きめにした方がNPSが上がります。

第31回世界コンピュータ将棋選手権 結果報告

「dlshogi with GCT」として、第31回世界コンピュータ将棋選手権に参加しました。
本日は予選2日目で、dlshogiはシードのため2日目からの参加でした。
上位8チームが決勝進出になります。

結果は、30チーム中14位と決勝進出ならず残念な結果でした。

昨年の電竜戦で、dlshogiを使用したGCTが優勝したため、ディープラーニング勢の躍進が期待されていましたが、
決勝進出は、NNUE系が7チームという結果になりました。

唯一PALがディープラーニングで、決勝に進出しています。
（決勝に進出したRyfamateはdlshogiとやねうら王(NNUE)の合議のようです。）

dlshogiが振るわなかった理由について

電竜戦やfloodgateに比べると持ち時間が長いことが関係している

dlshogi(GCT)は、floodgate（10分10秒加算）では大会で使用したGPUより世代が古いV100×8（gct_model-0000225kai_v100x8）で、レーティング4430と水匠4（Suisho4_TR3990X）とほぼ互角になっています。
ローカルの持ち時間3分1秒加算の対局（たややん互換局面使用）でも、3GPUのdlshogiが40スレッドの水匠3改に対して、60%くらいの勝率になっていました。
GCTが優勝した電竜戦は、10分2秒加算でした。

今回の世界コンピュータ将棋選手権は、15分5秒加算のルールで、長い持ち時間になっています。

dlshogiは、Resnet10ブロック192フィルタという軽めのモデル（AlphaZeroは20ブロック256フィルタ）を使用して、指し手のみを学習しているため、長い持ち時間を活かしきれない条件だったと推測しています。

探索ノード数の上限をfloatの桁落ちの制約で3千万局面に設定しているため、上限に達することが多くありました。

また、指し手のみを学習している（AlphaZeroは方策の分布を学習する）ため、探索中の各局面で調べる手がかなり絞られており、探索の深さが60以上(多いときは90以上)になっていました。
持ち時間が長い分を、深さより幅方向に時間を使えた方が読み漏れが防げた可能性があります。

そのため、より大きなモデルの方が有効だったか、温度パラメータを調整する余地があったかもしれません。

戦型に弱点がある

振り飛車が得意なHoneyWaffleに負けたことから、相手が上手い振り飛車だと弱点がありそうです。
強化学習の初期局面には、中盤中心の5億と、たややん互換局面集を多く学習して、たややん互換局面集で勝率測定をしていたため、たややん互換以外の戦型に弱点があったかもしれません。

入玉宣言を最短で目指さい

最後のNovice戦では、ほぼ勝ちで入玉宣言を目指せる局面から、無駄な駒得で手数が伸びて引き分けになってしまいました。
入玉宣言できる局面で、狙いに行くにはどうするかは課題があります。

まとめ

最後の2週間は、かなり強化学習をがんばったのですが、結果が及ばす残念でした。
ディープラーニングはまだ伸びしろがあると考えているので、次の大会では結果が残せるように開発は続けたいと思っています。

決勝に行けなかったので需要があるかはわかりませんが、dlshogiのビルド済みバイナリとGCTのモデルは後日公開する予定です。
強化学習で生成したデータも公開を検討していますが、Googleドライブの無料枠に収まらない(圧縮しても50GBくらい必要)のでディスクをどうしようかと思っています。