将棋AIの進捗その51（floatの桁落ち）

dlshogiの現在の実装では、長時間思考して探索ノード数が大きくなった場合に、ノードにバックアップされる価値の合計がfloat型になっているため、誤差が許容できないという指摘をやねうらお氏から頂いた。

floatに[0,1]の価値の値を足し合わせていく場合に、桁落ちは当然気を付けるべきだが、ディープラーニングを使用している場合、探索ノード数それほど多くならないので、指摘されるまで意識していなかった。
しかし、現状ではGPUを8枚使用するような状況になったので、長時間思考で問題になっていた。

floatの桁落ち

floatの仮数部は23ビットなので、有効桁数は10進数で7桁となる。
数千万ノードをバックアップする場合は、有効桁数には収まらなくなる。

以下のようなプログラムでシミュレーションすることで精度を確かめられる。

#include <iostream>
int main()
{
	const float value = 0.5f;
	const int N = 50000000;
	float win = 0;
	for (int i = 0; i < N; ++i) {
		win += value;
		if ((i + 1) % 1000000 == 0)
			std::cout << i + 1 << "\t" << std::fixed << win << "\t" << win / (i + 1) << std::endl;
	}
}

valueを0.5として、足し合わせていくと、1700万あたりで合計が増えなくなり、平均の計算の誤差が拡大していっている。
f:id:TadaoYamaoka:20201211234852p:plain

valueを0.8とすると、もっと早くから誤差が現れる。
f:id:TadaoYamaoka:20201211234909p:plain

持ち時間が長い大会の条件では、無視できない誤差となっている。

対策

doubleにする

floatをdoubleに変更することが、簡単な対策となる。
先ほどのプログラムのwinの型をdoubleに変えると、平均は誤差なく0.5となる。
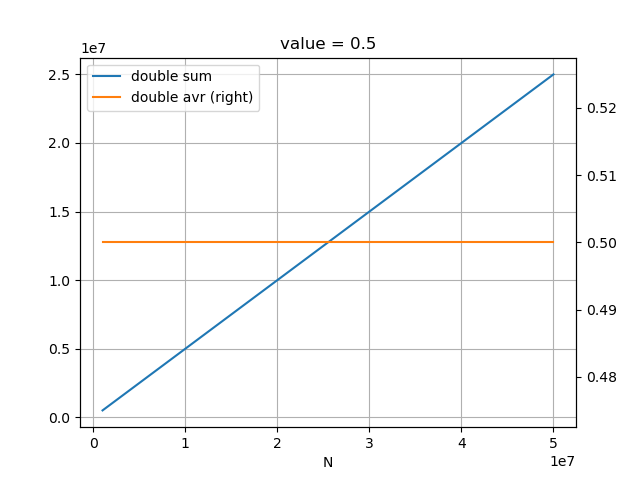
f:id:TadaoYamaoka:20201211235239p:plain

ただし、floatからdoubleにすることで、メモリ使用量が増える。

平均を保持する

他の方法として、ノードに合計を保持するのではなく、平均を更新する方法もある。
n回バックアップされたノードの価値の平均を $Q_n$ 、n回目にバックアップされる価値を $v_n$ とすると、n+1回目の平均は、
$\displaystyle Q_{n+1} = \frac{Q_n \cdot n + v_{n+1}}{n+1}$
で、計算できるので、平均の更新量は、
$\displaystyle Q_{n+1} - Q_n = \frac{v_{n+1} - Q_n}{n+1}$
で計算できる。

ただし、この方法で更新しようとすると、更新に変数を2つ使用するため、排他ロックが必要になる。
dlshogiは、可能な限りロックフリーになるようにatomicを使って実装しているため、この方式は採用したくない。
なお、Leela Chess Zeroはこの式を使用している。

また、この式を使用したとしても誤差がなくなるわけではない。
ノード数が増えると更新が無視されるようになるので誤差が広がらなくて済むだけである。

まとめ

長時間思考では誤差が無視できないことがわかったため、合計を保持する変数の型をdoubleに変更する対策を行うことにする。
現状でもメモリをかなり消費する実装になっているが、メモリ使用量がさらに増えることになる。
電竜戦で使用したAWSのA100インスタンスのメモリは1.1TBあるので、大会では問題にはならないだろう。

しかし、定跡作成で長時間思考する場合は、メモリの制約で探索ノード数を大きく増やせないという課題がある。
128GBで、5000万くらいが限度である。