TadaoYamaokaの開発日記

個人開発しているスマホアプリや将棋AIの開発ネタを中心に書いていきます。

Chainerで計算グラフの可視化

Chainer

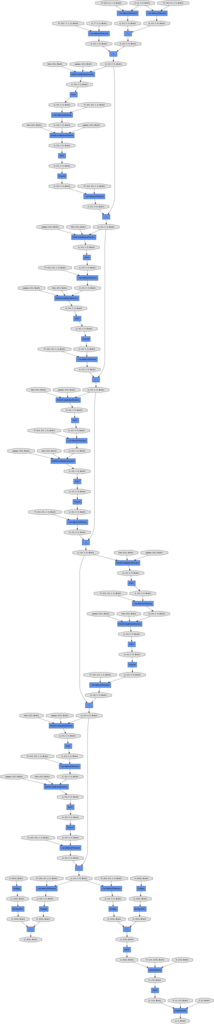
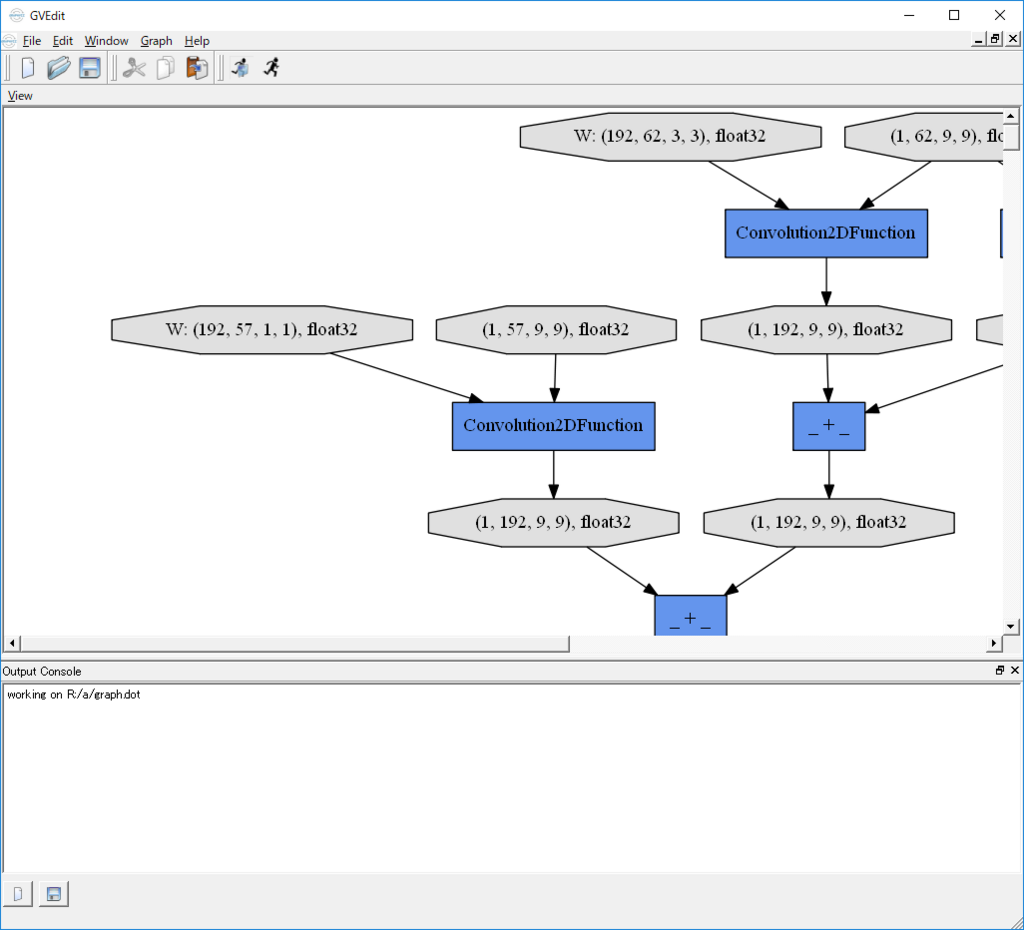
Chainerの計算グラフの可視化機能を使ったことなかったので使ってみた。

将棋AIのPolicy networkとValue networkを結合したWide ResNetを可視化してみた。

dotファイル出力

Visualization of Computational Graph — Chainer 7.8.1 documentation
このページの説明通り、モデルを構築し順伝播を実行し、出力のVariableを使用して、.dotファイルを作成する。

import numpy as np
from chainer import Variable
from chainer import Chain
import chainer.functions as F
import chainer.links as L
import chainer.computational_graph as c

FEATURES1_NUM=62
FEATURES2_NUM=57
MAX_MOVE_LABEL_NUM=101
k = 192
dropout_ratio = 0.1
fcl = 256 # fully connected layers
class PolicyValueNetwork(Chain):
    def __init__(self):
        super(PolicyValueNetwork, self).__init__(
            l1_1_1=L.Convolution2D(in_channels = FEATURES1_NUM, out_channels = k, ksize = 3, pad = 1, nobias = True),
            l1_1_2=L.Convolution2D(in_channels = FEATURES1_NUM, out_channels = k, ksize = 1, pad = 0, nobias = True),
            l1_2=L.Convolution2D(in_channels = FEATURES2_NUM, out_channels = k, ksize = 1, nobias = True), # pieces_in_hand
            l2=L.Convolution2D(in_channels = k, out_channels = k, ksize = 3, pad = 1, nobias = True),
            l3=L.Convolution2D(in_channels = k, out_channels = k, ksize = 3, pad = 1, nobias = True),
            l4=L.Convolution2D(in_channels = k, out_channels = k, ksize = 3, pad = 1, nobias = True),
            l5=L.Convolution2D(in_channels = k, out_channels = k, ksize = 3, pad = 1, nobias = True),
            l6=L.Convolution2D(in_channels = k, out_channels = k, ksize = 3, pad = 1, nobias = True),
            l7=L.Convolution2D(in_channels = k, out_channels = k, ksize = 3, pad = 1, nobias = True),
            l8=L.Convolution2D(in_channels = k, out_channels = k, ksize = 3, pad = 1, nobias = True),
            l9=L.Convolution2D(in_channels = k, out_channels = k, ksize = 3, pad = 1, nobias = True),
            l10=L.Convolution2D(in_channels = k, out_channels = k, ksize = 3, pad = 1, nobias = True),
            l11=L.Convolution2D(in_channels = k, out_channels = k, ksize = 3, pad = 1, nobias = True),
            l12=L.Convolution2D(in_channels = k, out_channels = MAX_MOVE_LABEL_NUM, ksize = 1, nobias = True),
            l12_2=L.Bias(shape=(9*9*MAX_MOVE_LABEL_NUM)),
            # value network
            l12_v=L.Convolution2D(in_channels = k, out_channels = MAX_MOVE_LABEL_NUM, ksize = 1, nobias = True),
            l12_2_v=L.Bias(shape=(9*9*MAX_MOVE_LABEL_NUM)),
            l13=L.Linear(9*9*MAX_MOVE_LABEL_NUM, fcl),
            l14=L.Linear(fcl, 1),
            norm1=L.BatchNormalization(k),
            norm2=L.BatchNormalization(k),
            norm3=L.BatchNormalization(k),
            norm4=L.BatchNormalization(k),
            norm5=L.BatchNormalization(k),
            norm6=L.BatchNormalization(k),
            norm7=L.BatchNormalization(k),
            norm8=L.BatchNormalization(k),
            norm9=L.BatchNormalization(k),
            norm10=L.BatchNormalization(k)
        )

    def __call__(self, x1, x2):
        u1_1_1 = self.l1_1_1(x1)
        u1_1_2 = self.l1_1_2(x1)
        u1_2 = self.l1_2(x2)
        u1 = u1_1_1 + u1_1_2 + u1_2
        # Residual block
        h1 = F.relu(self.norm1(u1))
        h2 = F.dropout(F.relu(self.norm2(self.l2(h1))), ratio=dropout_ratio)
        u3 = self.l3(h2) + u1
        # Residual block
        h3 = F.relu(self.norm3(u3))
        h4 = F.dropout(F.relu(self.norm4(self.l4(h3))), ratio=dropout_ratio)
        u5 = self.l5(h4) + u3
        # Residual block
        h5 = F.relu(self.norm5(u5))
        h6 = F.dropout(F.relu(self.norm6(self.l6(h5))), ratio=dropout_ratio)
        u7 = self.l7(h6) + u5
        # Residual block
        h7 = F.relu(self.norm7(u7))
        h8 = F.dropout(F.relu(self.norm8(self.l8(h7))), ratio=dropout_ratio)
        u9 = self.l9(h8) + u7
        # Residual block
        h9 = F.relu(self.norm9(u9))
        h10 = F.dropout(F.relu(self.norm10(self.l10(h9))), ratio=dropout_ratio)
        u11 = self.l11(h10) + u9
        # output
        h12 = self.l12(u11)
        h12_1 = self.l12_2(F.reshape(h12, (len(h12.data), 9*9*MAX_MOVE_LABEL_NUM)))
        # value network
        h12_v = self.l12_v(u11)
        h12_2 = F.relu(self.l12_2_v(F.reshape(h12_v, (len(h12_v.data), 9*9*MAX_MOVE_LABEL_NUM))))
        h13 = F.relu(self.l13(h12_2))
        return h12_1, self.l14(h13)

model = PolicyValueNetwork()

features1 = np.empty((1, FEATURES1_NUM, 9, 9), dtype=np.float32)
features2 = np.empty((1, FEATURES2_NUM, 9, 9), dtype=np.float32)
x1 = Variable(features1)
x2 = Variable(features2)

y1, y2 = model(x1, x2)

g = c.build_computational_graph([y1, y2])
with open('graph.dot', 'w') as o:
    o.write(g.dump())

dotファイルの可視化

dotファイルは、Graphvizを使って可視化する。

Graphvizをインストール後、binディレクトリをPATHに追加する。
以下のコマンドでdotをpngに変換する。

dot -Tpng graph.dot -o graph.png
生成されたpngファイル

f:id:TadaoYamaoka:20171025215710p:plain

灰色の横長の8角形が値、青の四角がFunctionを示している。
値は、畳み込みのパラメータはW:、バイアスはb:が頭に付いているので区別できる。

GUIツール

また、pngに変換しなくても、Graphvizに含まれるgveditというGUIツールを使うと、dotファイルを開いて表示できる。
f:id:TadaoYamaoka:20171025220435p:plain


TensorBoardと比べると見やすいとは言えないが、コーディングしたネットワークに誤りがないかの確認にはなると思う。

AlphaGo Zeroの論文を読む その5(ドメイン知識)

AlphaGo AlphaGo Zero コンピュータ囲碁

前回までで、実装に必要な内容についてほぼ解説しました。

今回は、補足的な内容です。

ドメイン知識

論文には以下の一文が記載されている。

Our primary contribution is to demonstrate that superhuman performance can be achieved without human domain knowledge.

「私たちの主な貢献は、人間の知識なしに超人的なパフォーマンスが達成できることを示すことです。」

人間の知識を用いないということが、この技術が囲碁に特化しない汎用的な技術であることを示している。
それを明確にするために、使用したドメイン知識を列挙している。

使用したドメイン知識

  1. 囲碁のルール：
    • シミュレーションの終端状態でのスコア付け
    • ゲームの終了条件
    • 各局面での合法手
  2. MCTSシミュレーション中にTromp-Taylorスコアリング(曖昧さの無いルール)を使用
  3. 19×19のボードであること
  4. 回転と反転しても囲碁のルールが不変であること

以上の点を超えるドメイン知識は使用していない。
以前のAlphaGoでは、rollout policyやtree policyにドメイン知識やヒューリスティックを利用していたが、rollout policyやtree policyは使用していない。

合法手は一切除外していない。
従来のプログラムでは合法手でも駄目を詰めるといった無駄な手を除外していたが、そのようなことはしていない。

ニューラルネットワークアーキテクチャは、画像認識の最新技術に基づいており、それに応じて訓練用ハイパーパラメータを選択した。
MCTS探索パラメータは、予備実験で訓練されたニューラルネットワークを使って自己対局を行い、ガウス過程により最適化した。

感想

技術の汎用性を示すために、あえてゼロから訓練を行っているように感じました。
部分的にドメイン知識を利用した方が強くなる可能性もあると思いますが、単に強くすることだけが目的ではないのでしょう。
逆に考えれば、囲碁の知識も有効活用すれば、強くすることに関しては上回る可能性はあると思います。
ただ、AlpaGo Zeroは以前のAlphaGoより強くなっているので、下手な囲碁の知識は入れない方が良いとは思います。


今回で終了します。

AlphaGo Zeroの論文を読む その4(自己対局)

AlphaGo Zero AlphaGo コンピュータ将棋 コンピュータ囲碁

その3の続き

自己対局パイプライン

自己対局パイプラインは、3つの主要な部分から構成される。

  1. 最適化
  2. 評価
  3. 自己対局

これらは並行で実行される。

最適化

  • ミニバッチサイズ：2,048 (32バッチずつ別々のGPUで実行)
  • ミニバッチデータは直近50万の自己対局のすべての局面からランダムでサンプリング
  • モーメントありのSGDで最適化(モメンタムパラメータ=0.9)
  • 学習率は以下の通り徐々に下げる
1000ステップ 学習率
0-400 10^{-2}
400-600 10^{-3}
>600 10^{-4}

損失関数を式にすると以下の通り
l=(z-v)^2 - {\bf \pi}^T log {\bf p} + c\|\theta\|^2
zは勝敗(-1,1)、vはvalue、{\bf \pi}はモンテカルロ木探索で求めた局面の遷移確率、{\bf p}はpolicyの遷移確率、\|\theta\|^2はネットワークのパラメータの2乗ノルム

  • 自己対局1,000回ごとにチェックポイントを設ける
  • チェックポイントで次の自己対局で使用するか評価を行う

評価

  • チェックポイントで現在の最良のネットワークと比較して評価する
  • モンテカルロ木探索アルゴリズムで最良のネットワークと400回対局を行う
  • 1手1,600シミュレーション
  • 温度パラメータは\tau \to 0とする(最大の訪問回数のノードを選択)
  • 最良のネットワークに55%以上勝利した場合、それを最良のネットワークとし、その後の自己対局で使用する

自己対局

  • 評価で選択した最良のネットワークを使ってデータを生成する
  • 各イテレーションでは、25,000ゲーム、1手1,600シミュレーションのモンテカルロ木探索で自己対局を行う

  • 各ゲームの最初の30手は温度\tau=1に設定する(訪問回数の応じた確率で着手し、局面にバリエーションを持たせる)

  • 残りの手は、温度\tau \to 0に設定する
  • ルートノードの事前確率にディリクレノイズを加える
  • 具体的には、P(x,a)=(1-\epsilon)p_a + \epsilon \eta_a, \eta \sim Dir(0.03), \epsilon=0.25
  • このノイズは、全ての手を試すために行うが、探索することで悪手は選択されなくなる

  • 計算資源を節約するため、明らかに負けの場合投了する
  • 閾値は誤認率を5%以下に保つように自動的に決定する
  • 誤認率を測定するため10%のゲームは終局までプレイする

将棋AIに応用する際の考察

損失関数について

policyの交差エントロピーは、式では教師データの指し手ではなく、遷移確率\piを使用していますが、温度パラメータを0にして自己対局しているので、実際は打ち手のみを学習することになるので、教師データとして打ち手をone hotベクトルとしたsoftmax交差エントロピーを使っていると思われます。

valueの損失には平均二乗誤差が使われています。
出力の活性化関数がtanhの場合は、交差エントロピーは負の値に使えないので、平均二乗誤差を使用していると思われます。
報酬が(-1,1)の単位スケールなのでvalueの平均二乗誤差とpolicyの交差エントロピーと同じ重みにするのは合理的だと、書かれていましたがちょっと意味が分かりませんでした。

なお、将棋AIでは、評価関数の出力にsigmoidを使用して、損失には交差エントロピーを使うのが主流になっています。

温度パラメータについて

局面のバリエーションを増やすために、自己対局の最初30手は温度パラメータが調整されています。
将棋AIでは、初期局面集を使って局面バリエーションを増やすことが行われています。
初期局面集の質が良ければその方がバリエーションを増やすには良いと思います。
初期局面集から開始して温度パラメータ調整ありで、数手を指すのが良いかもしれません。

残りの手は、温度パラメータを0にして最大訪問回数のノードを選択しています。
それではpolicyが予測する限られた手以外を探索しなくなるので、ルート局面のみノイズが加えられています。
policyは読み抜けをなくすこと重要なので、ノイズを加えることで対策しているようです。
ルート局面以外にもノイズを加えると探索の幅が広がりすぎるので、ルート局面のみに限定しています。
ノイズを加えることで、ついでにある程度打ち手にランダム性を加えることもできます。

ディリクレノイズについて、K次元のディリクレ分布は、
Dir({\bf p}|{\bf \alpha})=\frac{\Gamma(\sum_{k=1}^K \alpha_k)}{\prod_{k=1}^K \Gamma(\alpha_k)} \prod_{k=1}^K p_k^{\alpha_k-1}
で表されるので、出力ラベル数を次元としたディリクレ分布に従って生成した値をノイズに加えるということだと思います。
（合っているか自信がありません。間違っていたら教えてください。）

投了の閾値について

投了の閾値を自動で決定しているのはよく考えられていると思いました。
自分なら適当に決めていると思います。

対局数について

モンテカルロ木探索で自己対局をするには相当な時間がかかります。
個人で試そうと思ったらどこかで割り切りが必要そうです。

続く

2017/10/24 追記

ディリクレ分布について、グラフにして確かめてみた。
Dir(0.03)をα=0.03の対称ディリクレ分布と解釈すると、2次元の場合グラフは以下のようになる。
f:id:TadaoYamaoka:20171024210134p:plain

octaveで以下のようなスクリプトでプロットした。

alpha = [0.03 0.03];
x1 = linspace(0,1,101);
x2 = linspace(0,1,101);
[X1, X2] = ndgrid(x1, x2);
bad = (X1+X2 > 1 | X1+X2 < 0.98); X1(bad) = NaN; X2(bad) = NaN;

betaConst = exp(sum(gammaln(alpha))-gammaln(sum(alpha)));
F = (X1.^(alpha(1)-1) .* X2.^(alpha(2)-1)) / betaConst;

figure, surf(X1,X2,F,'EdgeColor','none');
xlabel('x1'); ylabel('x2'); zlabel('f(x1,x2)');

参考：
http://jp.mathworks.com/matlabcentral/newsreader/view_thread/139363


また、以下のようなスクリプトで5次元のディリクレ分布に従ってランダムに値を10個生成すると、以下のような値が生成された。

function r = drchrnd(a,n)
% take a sample from a dirichlet distribution
p = length(a);
r = gamrnd(repmat(a,n,1),1,n,p);
r = r ./ repmat(sum(r,2),1,p);
endfunction

A = drchrnd([0.03 0.03 0.03 0.03 0.03], 10)

参考：
To Generate Random Numbers from a Dirichlet Distribution | Yi Wang's Tech Notes

生成された値

  6.9672e-006  7.3486e-014  1.0742e-012  1.1276e-047  9.9999e-001
  5.5256e-009  1.5200e-037  9.9999e-001  6.5353e-006  4.2202e-034
  9.9999e-001  5.9592e-006  6.0206e-009  4.5226e-014  2.7251e-012
  2.3452e-025  5.0914e-011  9.9862e-018  1.0000e+000  2.7700e-043
  1.0641e-033  2.6900e-015  3.5634e-008  4.1919e-001  5.8081e-001
  1.5973e-010  2.2561e-010  1.8230e-023  6.8685e-045  1.0000e+000
  1.2859e-044  7.1633e-009  8.1942e-005  2.2902e-019  9.9992e-001
  7.8554e-001  7.7956e-018  1.4490e-005  2.1445e-001  3.6593e-023
  1.8477e-006  6.7389e-014  9.9992e-001  2.3746e-005  5.3420e-005
  3.8418e-039  2.9569e-011  9.9991e-001  9.9550e-025  9.3844e-005


以上の結果から、α=0.03のディリクレ分布はどれか一つの要素が1になり、他が0になるような分布になっていることがわかる。
つまり、ルートノードではどれか一つの手をランダムで選びやすくしている。
実装上は、ディリクレ分布を計算しなくてもランダムで1手を選んでその手のみη=1にしても問題ないかもしれない。

AlphaGo Zeroの論文を読む その3(探索アルゴリズム)

AlphaGo AlphaGo Zero コンピュータ囲碁

その2の続き

今回は対局時の探索アルゴリズムについてです。

探索アルゴリズム

対局時はpolicyとvalueを使ったモンテカルロ木探索(APV-MCTS)を使用する。
探索は複数スレッドで並列に行う。

探索木の各ノードsは以下の情報を持つ。

N(s,a) 行動aの訪問回数
W(s,a) 行動aの行動価値の合計
Q(s,a) 行動aの行動価値の平均
P(s,a) 行動aの事前確率

選択

展開済みノードの選択は、以前のAlphaGo(Fan Huiバージョン)と同じPUCTアルゴリズムを使う。

PUCTアルゴリズム

UCTアルゴリズムをpolicyを使って拡張したアルゴリズム。
UCB1に代わって以下の式を使用する。
Q(s_t,a)+U(s_t,a)
この値が最大となる行動aを選択する。
Q(s,a)はvalueから算出される(後述)。
U(s,a)は、policyの遷移確率P(s,a)を事前確率として使用した以下の式で計算される。
U(s,a)=c_{puct} P(s,a) \frac{\sqrt{\sum_b N(s,b)}}{1+N(s,a)}
c_{puct}は定数で、具体的な値は記載されていない。
以前のAlphaGoでは5が使われていた。

展開と評価

末端ノードLに到達したら、局面評価用キューに追加する。
キューに追加する際、8つの対称(反転、回転)な局面から1つランダムに選ぶ。

キューが8たまるとミニバッチを実行する。評価が完了するまで探索スレッドはロックする。
評価が完了すると、ノードを展開し、以下の値で初期化する。
N(s_L,a)=0, W(s_L,a)=0, Q(s_L, a)=0, P(s_L,a)=p_a
p_aはpolicyの出力値。

バックアップ

末端ノードからルートノードまで、訪問した順を逆にたどって、以下の通り各ノードを更新する。

訪問回数N(s,a)をインクリメントする。
N(s_t,a_t)=N(s_t,a_t)+1

行動価値を更新する。
W(s_t,a_t)=W(s_t,a_t)+v
vは、末端局面の評価で出力されたvalue。

行動価値の平均を更新する。
Q(s_t,a_t)=\frac{W(s_t,a_t)}{N(s_t,a_t)}

なお、訪問回数は、複数スレッドで同一局面を探索しないように、バーチャルロス(訪問回数を先にインクリメントしておく)を使用する。

打ち手決定

探索終了後、ルートノードの訪問回数から遷移確率を計算する。
\pi(a|s_0)=\frac{N(s_0,a)^{1/\tau}}{\sum_b N(s_0,b)^{1/\tau}}
\tauは温度パラメータ。温度が低いと差が開き、温度が高いと均一になる。0の場合は常に最大の手を選択する。

選択したノードの子ノードは次のステップで再利用する。
それ以外のノードとその子ノードは破棄する。

ルートノードのvalueと最善手を選んだ後の局面のvalueが閾値以下の場合、投了する。

以前のAlphaGoとの比較

以前のAlphaGoと比較して、rolloutを使用しないことが主要な違い。

以前のAlphaGoでは、policyの計算中に線形関数を使用した軽量のtree policyを使用し、また、valueの計算中に軽量のrollout policyを使用してrolloutを行ってvalueとrolloutの平均を報酬としていましたが、単純にニューラルネットワークの実行を待つようになっています。

将棋AIに応用する際の考察

rolloutを使用しないPUCTアルゴリズムが将棋AIでもある程度有効であることは、同様アルゴリズムを使用しているdlshogiがfloodgateでrating 2700になっていることで確かめています。
policyとvalueの精度が高くなれば、PUCTアルゴリズムを使ってまだ強くなる余地があると考えています。

評価する局面を8対称からランダムで選んでいるのは面白いと思いました。
精度をあまり落とさずにランダム性を持たせることができます。
将棋の場合は初期局面に対称性がない(飛車、角の位置が違う)ので対称な局面を考慮してもあまり意味がないと思われるので、この手法は使えなさそうです。

末端局面の初期化の際、dlshogiでは、W(s_L,a)=v, Q(s_L, a)=vとしていましたが、vを行動価値ととらえるとAlphaGo Zeroの方が正しい初期化の気がしました。

打ち手の決定は、最大の訪問回数の手を選択しないで、遷移確率に従っているのは自己対局で訓練データを生成する際はより適切と思いました。
プレイヤーとの対局時は、最大の訪問回数の手を選んでもよいと思います。

続く

コマンドプロンプトのカラースキーム変更

Windows

18日から提供開始されたWindows 10 Fall Creators Updateを適用しました。

今バージョンからコマンドプロンプトのカラースキーム変更になるということです。
今までコマンドプロンプトの青の文字が非常に読みづらく、Bash on Windowsを使うようになってから特にストレスを感じるようになりました。
なのでカラースキームの変更はうれしいですね。

適用後さっそくコマンドプロンプトで確認してみたところ、あれ？変わってない？
どうやらクリーンインストールしないと変わらないようですorz

後から変えたい場合は、ツールが提供されていました。
Creators Update適用しなくても変更できたのか。

Introducing the Windows Console Colortool - Windows Command Line
こちらからツールをダウンロードできます。

コマンドプロンプトのカラースキームの変更

colortool.exe -c

で現在の色が確認できます。

colortool.exe -d <スキーマ名>

で変更できます。
反映するにはコマンドプロンプトの再起動が必要です。

各カラースキームの色

変更前

f:id:TadaoYamaoka:20171021113621p:plain

campbell

f:id:TadaoYamaoka:20171021113743p:plain

campbell-legacy

f:id:TadaoYamaoka:20171021113928p:plain

OneHalfDark

f:id:TadaoYamaoka:20171021114021p:plain

OneHalfLight

f:id:TadaoYamaoka:20171021114102p:plain

solarized_dark

f:id:TadaoYamaoka:20171021114143p:plain

solarized_light

f:id:TadaoYamaoka:20171021114227p:plain

deuteranopia

f:id:TadaoYamaoka:20171021114438p:plain

Bash on Windowsのカラースキームの変更

これで、Bash on Windowsのlsの結果などが見やすくなると思ってBash on Windowsを起動したら、Bash on Windowsには反映されていませんでしたorz
Bash on Windowsのカラースキームを変更するには、コンソールのプロパティ→画面の色から手作業で設定する必要があります。
コマンドプロンプトのカラースキームを変更してから、コマンドプロンプトのプロパティ→画面の色と同じRGBの値に設定すればよいです。
f:id:TadaoYamaoka:20171021121033p:plain
色のパレットを選択して、赤、緑、青の数値をコマンドプロンプトと同じに設定すればよいです。
パレットの色を変更後、元のパレットの位置を選択しなおしてからOKを押しましょう(ラジオボタンで画面の背景を選んでいる場合は一番左)。

これで、青の文字が見やすくなりました。

変更前

f:id:TadaoYamaoka:20171021121204p:plain

変更後

f:id:TadaoYamaoka:20171021121323p:plain

AlphaGo Zeroの論文を読む その2(ネットワーク構成)

AlphaGo AlphaGo Zero コンピュータ囲碁 コンピュータ将棋

前回に続いてAlphaGo Zeroの論文についてです。

ネットワーク構成

入力特徴

  • 19×19の2値画像を17枚
  • 8枚は現在のプレイヤーの石の座標を示す2値画像、8手分
  • 8枚は相手のプレイヤーの石の座標を示す2値画像、8手分
  • 1枚は現在のプレイヤーの石の色を示す全て0か1の画像

履歴を必要とするのは囲碁にはコウがあるため。
現在のプレイヤーの石の色が必要なのは囲碁にはコミがあるため。

以前(Fan Huiバージョン)のAlphaGoでは入力特徴に、呼吸点やシチョウなどの囲碁の知識を含む48の特徴を使用していましたが、石の座標情報のみになっています。

ニューラルネットワーク構成

入力層

1層の畳み込み層で以下の構成

  1. 畳み込み 3×3のフィルター、256
  2. Batch Normalization
  3. 活性化関数

以前のAlphaGoは5×5のフィルター192でしたが、より数が増えています。
Batch Normalizationも以前はありませんでした。
活性化関数には、具体的に何の関数を使っているか記載がありません。
以前はReLUだったので、同じと思われます。

中間層

19個、または39個の残差ブロック
1つの残差ブロックは以下の構成

  1. 畳み込み 3×3のフィルター、256
  2. Batch Normalization
  3. 活性化関数
  4. 畳み込み 3×3のフィルター、256
  5. Batch Normalization
  6. 残差入力の接続
  7. 活性化関数

図示すると以下のようになります。
f:id:TadaoYamaoka:20171021091056p:plain

オーソドックスなResNetのブロックです。
残差ブロックの数は、はじめは19個で自己対局を行い、最終的に39個としています。

出力層

ネットワークを分岐して、PolicyとValueを出力します。
Policyの出力は以下の構成

  1. 畳み込み 1×1のフィルター、2
  2. Batch Normalization
  3. 活性化関数
  4. 19×19(打ち石の座標)+1(pass)を示す362ノードの全結合層でlogit probabilitiesを出力

logit probabilitiesはsoftmax関数の入力となる値で、softmax関数の出力が打ち手の確率を示します。

以前のAlphaGoでは1×1のフィルター1の出力をlogit probabilitiesとしていましたが、全結合層が加わっています。

Valueの出力は以下の構成

  1. 畳み込み 1×1のフィルター、1
  2. Batch Normalization
  3. 活性化関数
  4. 256ノードの全結合層
  5. 活性化関数
  6. tanh関数で勝率を示すスカラー値を出力する1ノードの全結合層

Batch Normalization以外は、以前のAlphaGoと同じ構成です。

将棋AIに応用する際の考察

入力特徴について

将棋AIに応用する際には、将棋には駒の取り合いや千日手があるので、入力特徴の履歴の情報は有用と思われます。
現在のプレイヤーの石の色の情報は、将棋にはコミがないので不要かもしれません。

ニューラルネットワーク構成について

ResNetが将棋でも有用であることは、以前の実験で確かめています。
私の実験では5ブロックで192のフィルターでしたが、39層で256のフィルターはかなりの規模です。
試そうと思うと学習時間は相当かかるので覚悟が必要そうです。

PolicyとValueの同時出力について

将棋でもマルチタスク学習が有用であることも以前の実験で確かめています。

出力層の構成について

Policyの出力に全結合層が加わっています。
この構成にした理由は書かれていませんが、この方が精度が上がるということでしょうか。
将棋でも有用か試してみようと思います。
1×1のフィルターを出力としていると、移動できない座標もラベルとする必要がありましたが、全結合を使うなら、出力ラベル数は減らせるのでその効果もでるかもしれません。

Valueには以前のAlphaGoと同様にtanh関数が使われていますが、コンピュータ将棋では評価関数の出力にsigmoidを使う方が主流ですね。
sigmoidでも大差はないと思っていますが、tanh関数を使った方がよい理由とかあるのでしょうか。
分かる人がいらっしゃたら教えてもらえると助かります。

続く

AlphaGo Zeroの論文を読む

AlphaGo AlphaGo Zero コンピュータ囲碁

今日のAlphaGo Zeroのニュースは衝撃でした。

将棋AIで方策勾配で強化学習を行ったときは、発散してうまくいかなかったので
教師データで最初に訓練が必要と思っていました。
それが、自己対局のみで強くできるとは驚きです。

論文が公開されたので、使われたテクニックを調べていきたいと思います。

Mastering the game of Go without human knowledge | Nature

まだ全部読んでいませんが、ざっくり初めの方を読んで以下の特徴があるようです。

  1. PolicyとValueを1つのネットワークで出力する
  2. Batch Normalisationと非線形の活性化関数を使用したResidual Network(ResNet)
  3. モンテカルロ木探索による自己対局で生成した各局面の打ち手と、勝敗結果を訓練データに使用する
  4. モンテカルロ木探索はノードを1回訪問したら展開する
  5. rolloutは使用しない
  6. 訓練の損失関数にはValueの平均二乗誤差とPolicyの交差エントロピー損失の和を同じ重みで使う
  7. L2正則化をする


Methodに自己対局と訓練方法について、かなり詳細に書かれていますので、
理解した内容を少しずつ書いていこうと思います。


おそらくこの方法は将棋AIにも応用可能と思われます。

PolicyとValueを1つのネットワークで出力すのは、
自分の将棋AIでも行っていて効果を確かめていましたが、
別々のネットワークの方が実は良いのではと思っていましたので、
自信が得られました。

モンテカルロ木探索の部分はrolloutを使わず1回で展開するのは、
自分の将棋AIと基本は同じ方法ですが、
ボルツマン分布の温度パラメータを動的に変えているようです。
将棋でも効果があるか実験したいところです。

続く。。。

AlphaGo Zeroの論文を読む その2(ネットワーク構成) - TadaoYamaokaの開発日記
AlphaGo Zeroの論文を読む その3(探索アルゴリズム) - TadaoYamaokaの開発日記
AlphaGo Zeroの論文を読む その4(自己対局) - TadaoYamaokaの開発日記
AlphaGo Zeroの論文を読む その5(ドメイン知識) - TadaoYamaokaの開発日記