hyperoptを使ってみる

ほぼ自分用のメモです。

前回ベイズ最適化で探索パラメータの最適化を試したが、ぽんぽこなどが使っているhyperoptも試してみた。

最適化する目的変数

テスト用に、説明変数が2つで、極大値が複数ある少々複雑な関数を用意した。

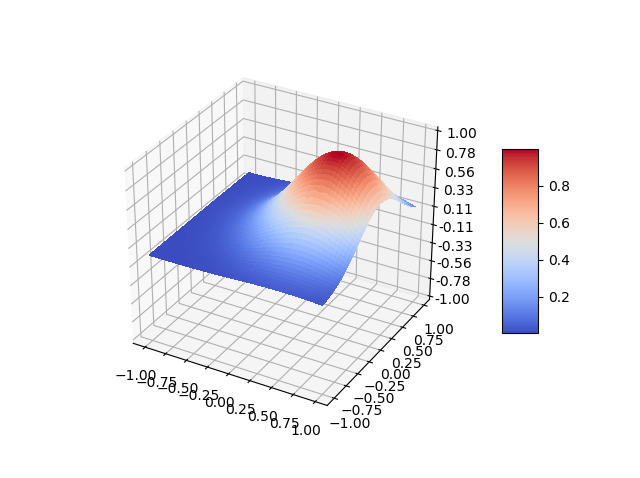
Z = 10**(-(X-0.1)**2)*10**(-Y**2)*np.sin(5*X)*np.sin(3*Y)

グラフにすると、以下のような形になる。

from mpl_toolkits.mplot3d import Axes3D

import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter
import numpy as np

fig = plt.figure()
ax = fig.gca(projection='3d')

X = np.arange(-1, 1, 0.01)
Y = np.arange(-1, 1, 0.01)
X, Y = np.meshgrid(X, Y)
Z = 10**(-(X-0.1)**2)*10**(-Y**2)*np.sin(5*X)*np.sin(3*Y)

surf = ax.plot_surface(X, Y, Z, cmap=cm.coolwarm,
                       linewidth=0, antialiased=False)

ax.set_zlim(-1.0, 1.0)
ax.zaxis.set_major_locator(LinearLocator(10))
ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f'))

fig.colorbar(surf, shrink=0.5, aspect=5)

plt.show()

この関数は、x = 0.28、y = 0.36付近で最大となる。

Z.argmax() # 27328
X.flatten()[27328] # 0.28000000000000114
Y.flatten()[27328] # 0.3600000000000012

hyperoptで最適化

hyperoptでは、以下のようにして目的変数が最大となるパラメータの探索を行う。

from hyperopt import fmin, tpe, hp

def objective(args):
    x, y = args
    return -10**(-(x-0.1)**2)*10**(-y**2)*np.sin(5*x)*np.sin(3*y)

space = [hp.uniform('x', -1, 1), hp.uniform('y', -1, 1)]

best = fmin(objective,
    space,
    algo=tpe.suggest,
    max_evals=100)

print(best)

hyperoptは最小値を探索するので、objectiveのreturnをマイナスにしている。

探索空間は、spaceにx、yそれぞれ[-1, 1]の範囲と定義している。hp.uniformは、一様ランダムにサンプリングした点から探索を行うことを意味する。

実際の探索の処理は、fminで行っている。引数のalgoにtpe.suggestを指定することで、「Tree of Parzen Estimators (TPE)」というアルゴリズムで探索が行われる（TPEがGPと比べてどうなのかといった理論的な話はよくわかっていない）。

実行結果

max_evalsを20ずつ増やしていった結果は、以下のようになった。

max_evals	x	y
20	0.39556414532440365	0.20875085952399286
40	0.3202657168213312	0.42527827006887997
60	-0.24148461859260986	-0.36080178232006715
80	0.37880403950167435	0.29472084021122946
100	0.2611536044253473	0.39531968048635835

100の試行でだいたい正解に近づいている。

追試

もっと単純な関数でも試してみた。

Z = 10**(-(X-0.5)**2)*10**(-(Y-0.2)**2)

この関数は、x=0.5、y=0.2で最大となる。

max_evalsを20ずつ増やしていった結果は、以下のようになった。

max_evals	x	y
20	0.3443597966317844	0.23786682969927742
40	0.38271437610741593	0.14961016637448996
60	0.49909182531107105	0.16338851488579612
80	0.47974941506728047	0.16023365584782412
100	0.5242348907635725	0.19484332282113948

今度は、60回でだいたい正解に近づいている。

hyperoptでは、サンプリングの手法としてuniform以外にも正規分布に基づくnormなども指定できるので、大雑把に調べてから正規分布で調べた方が効率的に探索できるかもしれない。

追試2

比較のため、ランダムサーチでも測定してみた。

from hyperopt import rand

best = fmin(objective,
    space,
    algo=rand.suggest,
    max_evals=100)

1つ目の関数

max_evals	x	y
20	0.3385365523415862	0.07397186373359554
40	-0.23970049764740975	-0.33954484250904127
60	0.27495652472338383	0.3548873522022511
80	0.28471503714642177	0.563064953585914
100	0.35214511978226337	0.2684189656435647

2つ目の関数

max_evals	x	y
20	0.3742602732502782	0.31675423601984165
40	0.6009004093795294	0.14050923510882107
60	0.716162366548053	0.11912978009135555
80	0.34036595940517334	0.3499254601398716
100	0.5909165567905033	0.022329294838111302

1つめの関数の60回で正解に近くなっているが、それ以外は近づいていない。
2つ目の関数も正解に近づいていない。
実験した2つの関数では、TPEの方が効率的に探索できていると言える。