optunaを使ってみる

昨日試したhyperoptと同じことをoptunaで試してみた。

探索する関数の形

hyperoptで試したものと同じ、2つの説明変数で、極大値が複数ある関数

Z = 10**(-(X-0.1)**2)*10**(-Y**2)*np.sin(5*X)*np.sin(3*Y)

optunaによる最適化

optunaでは以下のようにしてパラメータの最適化を行う。

import numpy as np
import optuna

def objective(trial):
    x = trial.suggest_uniform('x', -1, 1)
    y = trial.suggest_uniform('y', -1, 1)
    return -10**(-(x-0.1)**2)*10**(-y**2)*np.sin(5*x)*np.sin(3*y)

study = optuna.create_study()
study.optimize(objective, n_trials=100)

結果は、以下のように出力される。

[I 2018-12-18 22:22:38,234] Finished a trial resulted in value: -0.26608404873345176. Current best value is -0.26608404873345176 with parameters: {'x': -0.4372236826385516, 'y': -0.42153119135705275}.
(略)
[I 2018-12-18 22:22:39,082] Finished a trial resulted in value: 0.23048800674448708. Current best value is -0.5864926930433219 with parameters: {'x': 0.284010530868015, 'y': 0.3078011551597313}.

試行1回に付きログが1行出力される。

hyperoptと比較するため結果を並べてみる。

hyperopt

試行回数	x	y
20	0.39556414532440365	0.20875085952399286
40	0.3202657168213312	0.42527827006887997
60	-0.24148461859260986	-0.36080178232006715
80	0.37880403950167435	0.29472084021122946
100	0.2611536044253473	0.39531968048635835

optuna

試行回数	x	y
20	-0.4372236826385516	-0.42153119135705275
40	0.2758835033984871	0.18587125262622836
60	0.284010530868015	0.3078011551597313
80	0.284010530868015	0.3078011551597313
100	0.284010530868015	0.3078011551597313

optunaの方が少ない試行で近づいている。正解はx = 0.28、y = 0.36付近だが、近い値になっている。

収束傾向

optunaは一度収束するとそれ以降同じ値になっている。
hyperoptの結果は、max_evalsを変更して測定し直しているので、途中で収束しているかは確認できていない。
そこで、Trialsを使って途中経過を確認してみた。

from hyperopt import Trials
trials = Trials()
fmin(objective,
    space,
    algo=tpe.suggest,
    max_evals=100,
    trials=trials)

trials.miscsに途中結果が保存されるので、途中結果を確認してみた。

試行回数	x	y
20	0.5420640699743933	0.5315515733903343
40	-0.5098469891667613	-0.438424969493291
60	0.03469969785010063	-0.040788916295743854
80	0.608071890102492	0.006584448401573517
100	0.30918481652031465	-0.1562913234242519

hyperoptは途中で収束することなく、新しい値を探索するようである。
試行回数が多いと正解に近づく可能性はあるが、optunaよりも収束が遅い傾向がありそうである。
逆に、optunaは収束すると新しい値は探索しないので、探索空間を狭めてさらに探索するとよさそうである。

追試

単純な関数でも試してみた。

Z = 10**(-(X-0.5)**2)*10**(-(Y-0.2)**2)

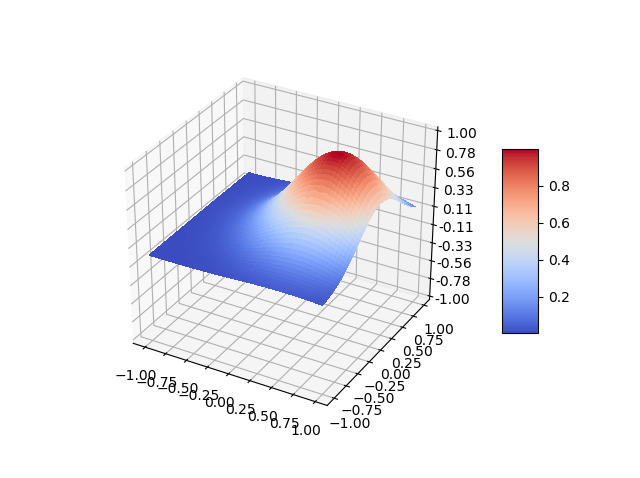
この関数は、x=0.5、y=0.2で最大となる。

hyperopt

試行回数	x	y
20	0.3443597966317844	0.23786682969927742
40	0.38271437610741593	0.14961016637448996
60	0.49909182531107105	0.16338851488579612
80	0.47974941506728047	0.16023365584782412
100	0.5242348907635725	0.19484332282113948

optuna

試行回数	x	y
20	0.45310859794747144	-0.04581641718039608
40	0.5736411512986137	0.28240726860174903
60	0.4378516591044338	0.21435567472136136
80	0.4378516591044338	0.21435567472136136
100	0.4378516591044338	0.21435567472136136

1つ目の関数と同じ傾向で、optunaは早く正解に近づいている。