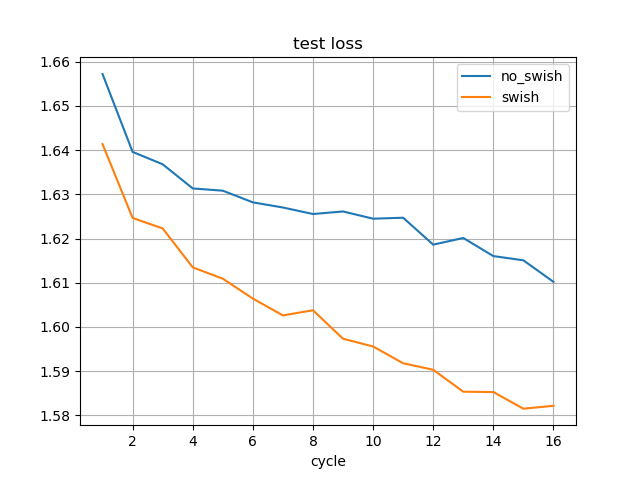
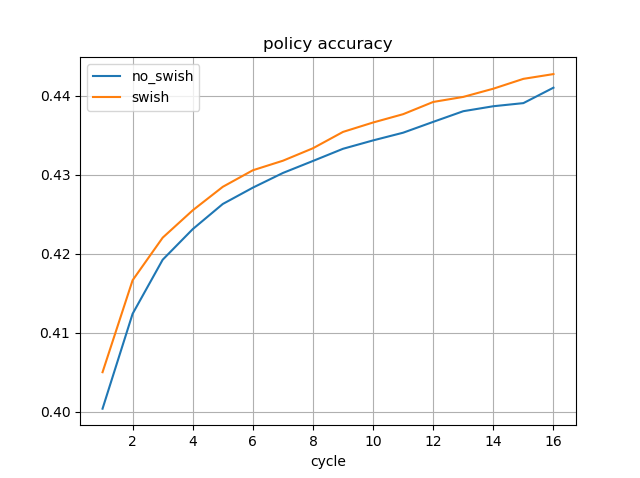
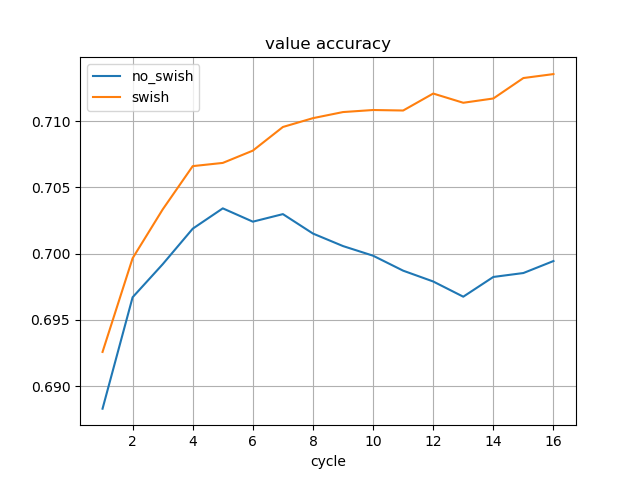
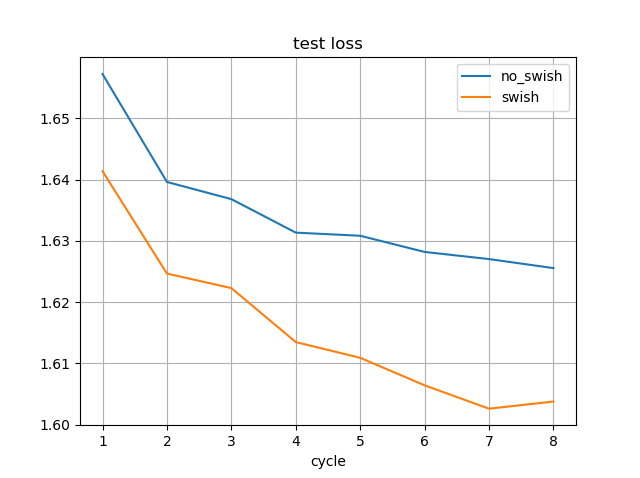
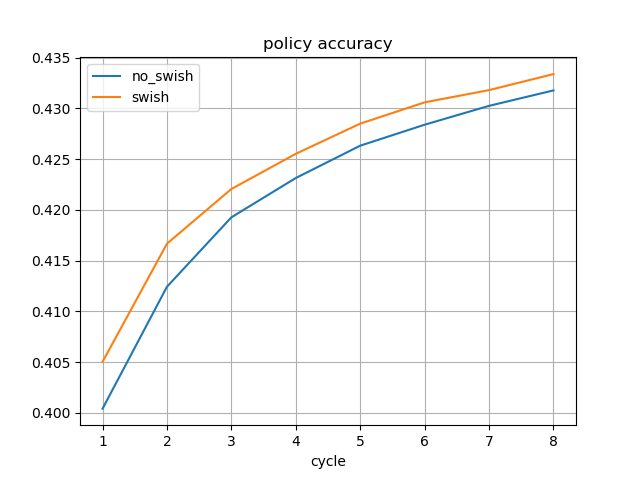
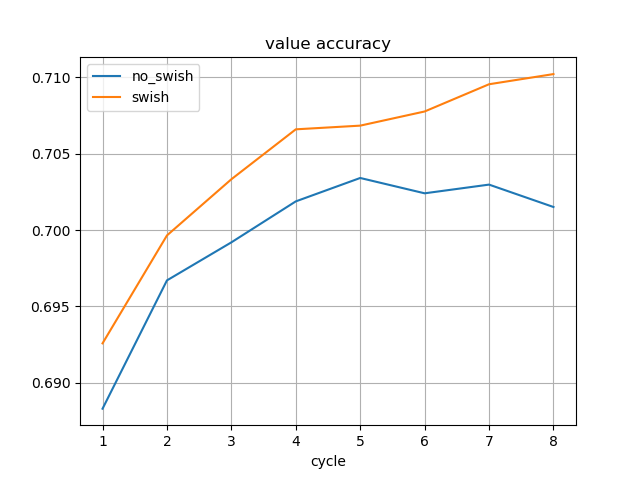
MCTSと思考時間と強さの関係について、dlshogiのデータが知りたいという要望があったので測定してみた。
測定条件
対戦相手は、最新のやねうら王をUbuntu 18.04のclangでビルドしたもの+水匠2の評価関数で、1000万ノード固定とする。
dlshogiは、最新のソースに、最新のモデル(WCSOC1からR+76くらい)を使用した。
測定環境は、CPU Xeon E5-2698 v4(2.20GHz)、GPU NVIDIA V100、Ubuntu 18.04(Docker)。
水匠2は2スレッド、dlshogiは3スレッド1GPUを使用し、思考時間を変えて測定。
思考時間は、1秒、2秒、3秒、4秒、8秒、16秒とした(8秒、16秒は測定中)。
ポンダーはなし。
256手で引き分け。
強さは、互角局面集を使用して、先後を交互に入れ替え、250戦行った結果で測る。
引き分けも考慮するため、勝率は、勝ちを1ポイント、引き分けを0.5ポイントとして、ポイントの合計/250で計算する。
水匠2は、評価値-10000で投了、dlshogiは、勝率1%で投了する。
eloレーティングは、水匠2のeloレーティングを0、 を勝率として、
を勝率として、

で計算する。
測定結果
| 思考時間(秒) |
勝ち |
引き分け |
勝率 |
R |
| 1 |
87 |
9 |
36.6% |
-95.44 |
| 2 |
132 |
7 |
54.2% |
29.25 |
| 3 |
158 |
3 |
63.8% |
98.44 |
| 4 |
165 |
2 |
66.4% |
118.33 |
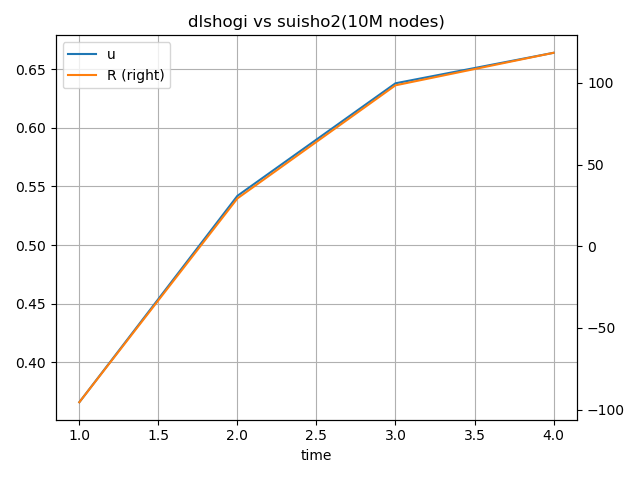
dlshogiの思考時間ごとの探索ノード数は、以下の通り。
| 思考時間(秒) |
探索ノード数(平均) |
探索ノード数(中央値) |
| 1 |
71971 |
61518 |
| 2 |
140604 |
121388 |
| 3 |
207204 |
179994.5 |
| 4 |
270545 |
232072 |
考察
dlshogiの思考時間を増やすことで、強さは対数に近い形で伸びているようだ。
もう少し先の形も確認すればはっきりしそうである(8秒、16秒のデータが測定できたら追記する)。
また、測定目的とは異なるが、水匠2の1000万ノードに対して、dlshogiは10万ノード(1/100)くらいで互角になることがわかった。
αβ探索での思考時間と強さの関係
αβ探索での思考時間と強さの関係についても調べた。
対戦相手は、上記と同様に水匠2の1000万ノード固定とする。
測定側は、水匠2 2スレッドで、思考時間を1秒、2秒、3秒、4秒、8秒、16秒とした(8秒、16秒は測定中)。
測定環境は、CPU Xeon Silver 4210 (2.20GHz)を使用した。
測定結果
| 思考時間(秒) |
勝ち |
引き分け |
勝率 |
R |
| 1 |
7 |
10 |
4.8% |
-518.96 |
| 2 |
18 |
15 |
10.2% |
-377.87 |
| 3 |
26 |
20 |
14.4% |
-309.64 |
| 4 |
55 |
18 |
25.6% |
-185.33 |
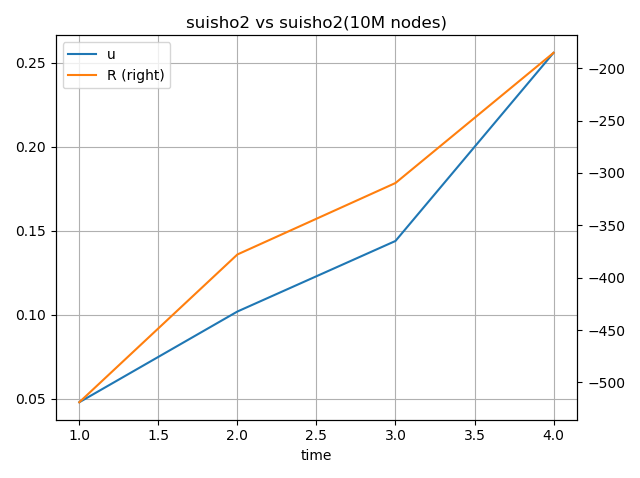
水匠2の思考時間ごとの探索ノード数は、以下の通り。
※ログから集計が面倒だったので1局面だけサンプリング
| 思考時間(秒) |
探索ノード数 |
| 1 |
1298863 |
| 2 |
2252468 |
| 3 |
4359210 |
| 4 |
5334843 |
考察
2スレッドで測定したため、探索ノード数が1000万ノードよりも低すぎて、右側を見ないと対数の関係なのかどうかが見れないデータになっていた。
スレッド数を8にして測定をやり直すことにする。
測定ができたら別途追記する。
まとめ
MCTSの思考時間と強さの関係は、対数の関係になりそうであることがわかった。
探索深さに対してゲーム木のサイズが指数関数的に増えることと関係していると思われる。
AlphaZeroの論文では、αβよりも思考時間に対する強さの伸びが高いことが報告されている。
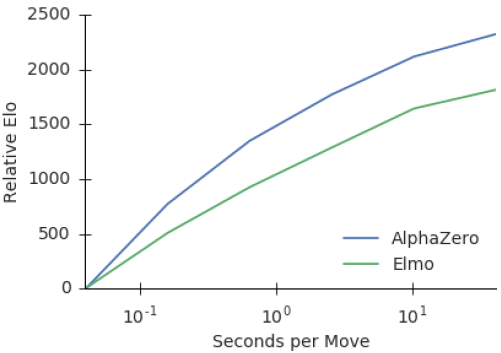
同じ対数的な伸びでも、伸び方に差がでている。
αβで思考時間を延ばした場合も測定をしようとしたが、今回は測定条件のミスで使えるデータがとれなかった。
測定できたら、別途記事にしたい。